公理化系统有,逻辑推理的基石

公理化系统：逻辑推理的基石

在数学、逻辑学以及哲学等领域，公理化系统扮演着至关重要的角色。它是一种通过定义一组基本假设（公理）和演绎规则，从这些基本假设出发，推导出一系列结论的方法。本文将探讨公理化系统的概念、重要性以及其在不同领域的应用。

一、公理化系统的定义与起源

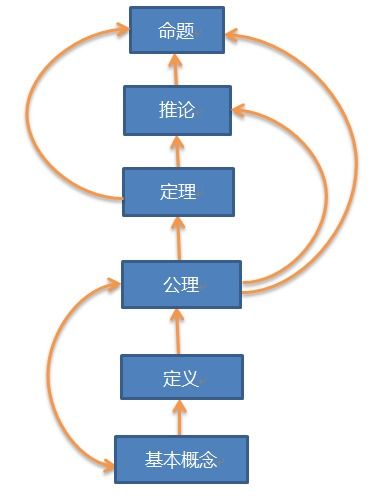
公理化系统起源于古希腊，最早由欧几里得在其著作《几何原本》中提出。欧几里得通过定义一组基本的几何公理，如“两点之间，线段最短”等，并在此基础上推导出一系列几何定理。这种通过公理推导出结论的方法，为后来的数学发展奠定了基础。

二、公理化系统的重要性

公理化系统的重要性体现在以下几个方面：

提供了一种严谨的推理方法：通过公理和演绎规则，可以确保推理过程的正确性，避免主观臆断和错误结论的出现。

简化了复杂问题：将复杂问题分解为基本假设和演绎规则，有助于我们更好地理解和解决这些问题。

促进了数学的发展：公理化系统为数学研究提供了坚实的理论基础，推动了数学的进步。

三、公理化系统在数学领域的应用

公理化系统在数学领域的应用广泛，以下列举几个例子：

几何学：欧几里得几何、非欧几何等，都是基于公理化系统建立的。

集合论：通过公理化系统，我们可以定义集合、关系、函数等基本概念，并研究它们的性质。

数理逻辑：公理化系统为逻辑推理提供了基础，有助于我们研究命题、证明和推理的有效性。

四、公理化系统在其他领域的应用

除了数学领域，公理化系统在其他领域也有广泛的应用，以下列举几个例子：

计算机科学：在编程语言、算法设计等领域，公理化系统有助于我们理解和验证程序的正确性。

经济学：公理化系统可以用于建立经济模型，分析市场行为和资源配置。

哲学：公理化系统为哲学研究提供了逻辑基础，有助于我们探讨道德、认识论等问题。

公理化系统作为一种严谨的推理方法，在数学、逻辑学以及哲学等领域发挥着重要作用。通过定义一组基本假设和演绎规则，我们可以从这些基本假设出发，推导出一系列结论。公理化系统不仅为各个领域的研究提供了理论基础，而且有助于我们更好地理解和解决复杂问题。