高阶系统的稳定性,高阶系统的稳定性概述

高阶系统的稳定性概述

在控制系统和信号处理领域，高阶系统稳定性是一个核心问题。高阶系统指的是那些阶数大于二阶的系统，它们在数学模型上通常表现为多项式方程。稳定性分析是确保系统在受到扰动后能够恢复到初始状态或稳定状态的关键步骤。本文将探讨高阶系统稳定性的基本概念、分析方法以及影响因素。

稳定性基本概念

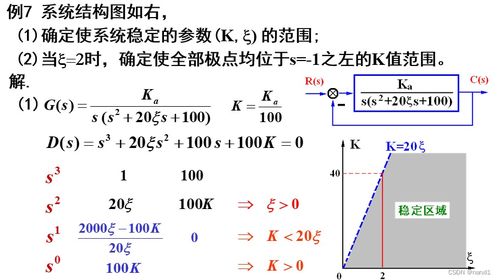
稳定性是系统在受到扰动后，能否回到或保持在初始稳定状态的能力。对于线性时不变系统，稳定性通常通过分析系统的传递函数或特征方程来判断。一个系统被称为BIBO（有界输入有界输出）稳定，如果对于任何有界输入信号，其输出信号也是有界的。

稳定性分析方法

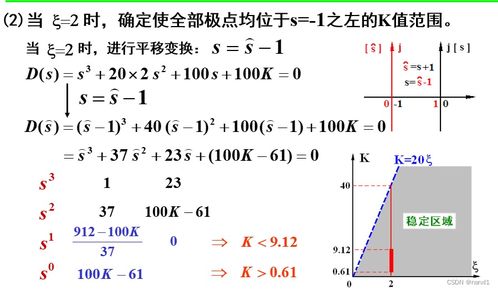
高阶系统的稳定性分析主要依赖于以下几种方法：

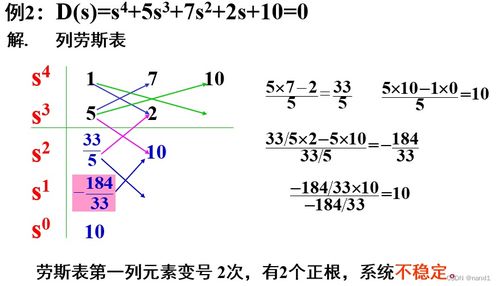
劳斯判据：劳斯判据是一种基于系统特征方程系数的稳定性判据，适用于线性时不变系统。通过分析特征方程的系数，可以判断系统是否稳定。

乃奎斯特判据：乃奎斯特判据是一种图形方法，通过绘制系统的Nyquist图来判断稳定性。这种方法适用于传递函数具有多个极点和零点的情况。

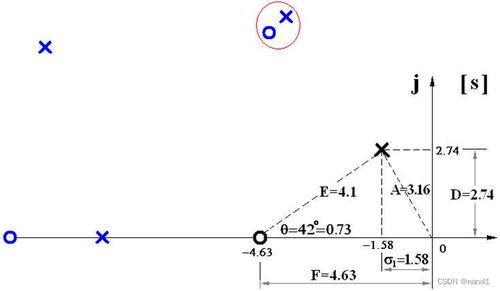
根轨迹图：根轨迹图是分析系统稳定性的一种方法，通过绘制系统传递函数的极点随系统参数变化而移动的轨迹来判断稳定性。

相角裕度和增益裕度：对于最小相位系统，相角裕度和增益裕度是衡量系统稳定性的重要指标。相角裕度表示系统在单位增益时的相位裕量，而增益裕度表示系统在单位相位裕量时的增益裕量。

高阶系统稳定性的影响因素

系统阶数：随着系统阶数的增加，系统的稳定性分析变得更加复杂，因为需要考虑更多的极点和零点。

系统参数：系统参数的变化会影响系统的传递函数，从而影响系统的稳定性。例如，增益参数的变化可能导致系统从稳定状态变为不稳定状态。

外部扰动：外部扰动是影响系统稳定性的另一个重要因素。系统设计时需要考虑外部扰动的影响，并采取措施提高系统的鲁棒性。

系统结构：系统结构的设计也会影响系统的稳定性。例如，引入反馈控制可以改善系统的稳定性。

高阶系统稳定性分析的应用

高阶系统稳定性分析在许多领域都有广泛的应用，包括：

控制系统设计：在控制系统设计中，稳定性分析是确保系统性能的关键步骤。

信号处理：在信号处理领域，稳定性分析用于设计滤波器和其他信号处理算法。

通信系统：在通信系统中，稳定性分析用于设计调制解调器和其他通信设备。

生物医学工程：在生物医学工程领域，稳定性分析用于设计医疗设备和生物传感器。

结论

高阶系统的稳定性分析是一个复杂而重要的课题。通过合理的设计和稳定性分析，可以提高系统的性能和鲁棒性。本文简要介绍了高阶系统稳定性的基本概念、分析方法以及影响因素，旨在为相关领域的研究和实践提供参考。