分数阶系统,探索非线性世界的新维度

分数阶系统：探索非线性世界的新维度

随着科学技术的不断发展，对复杂系统的理解和建模成为了一个重要的研究领域。分数阶系统作为一种新型的数学模型，因其能够更精确地描述现实世界中的物理现象，受到了越来越多的关注。本文将介绍分数阶系统的基本概念、研究现状及其在各个领域的应用。

一、分数阶微积分：分数阶系统的理论基础

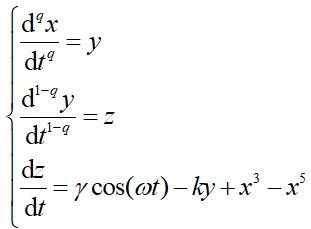
分数阶微积分是分数阶系统的基础，它是对传统整数阶微积分的扩展。在分数阶微积分中，导数和积分的阶数不再是整数，而是分数。这种扩展使得分数阶微积分能够更好地描述自然界中存在的复杂现象。分数阶微积分的基本概念包括分数阶导数、分数阶积分和分数阶微分方程。

二、分数阶系统的特点

与整数阶系统相比，分数阶系统具有以下特点：

更精确地描述现实世界中的物理现象

具有更丰富的动力学行为

能够处理系统中的记忆效应

具有更好的鲁棒性

三、分数阶系统的研究现状

分数阶系统的稳定性分析

分数阶系统的控制策略

分数阶系统的数值模拟

分数阶系统在各个领域的应用

四、分数阶系统在各个领域的应用

分数阶系统在各个领域都有广泛的应用，以下列举一些典型的应用场景：

生物医学：分数阶系统可以用于描述生物体内的复杂过程，如神经元活动、心脏跳动等。

机械工程：分数阶系统可以用于描述机械系统中的摩擦、磨损等非线性现象。

信号处理：分数阶系统可以用于信号处理中的滤波、去噪等任务。

控制理论：分数阶系统可以用于设计更鲁棒的控制策略，提高系统的性能。

分数阶系统作为一种新型的数学模型，在描述现实世界中的复杂现象方面具有独特的优势。随着研究的不断深入，分数阶系统将在各个领域发挥越来越重要的作用。本文对分数阶系统的基本概念、研究现状及其应用进行了简要介绍，旨在为读者提供一个关于分数阶系统的全面了解。

分数阶系统，分数阶微积分，非线性系统，稳定性分析，控制策略，应用领域