2自旋系统,自旋系统的基本概念

自旋系统的基本概念

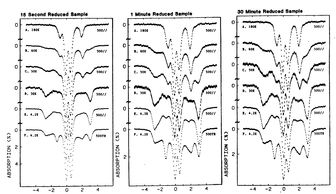
自旋系统是量子力学中的一个重要概念，它描述了微观粒子（如电子、原子核等）的角动量性质。在经典物理学中，角动量是描述物体旋转状态的物理量，而在量子力学中，角动量被量子化，即只能取特定的离散值。自旋系统就是研究这些量子化的角动量及其相关性质的理论体系。

自旋量子数的定义

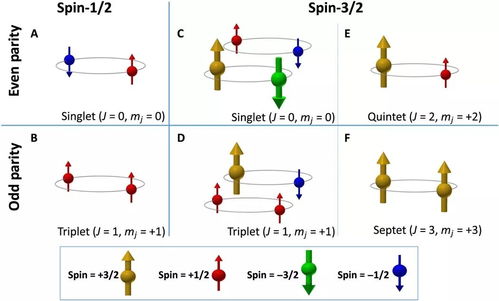
自旋量子数是描述自旋系统角动量大小的量子数，用符号s表示。自旋量子数可以是整数或半整数，具体取决于粒子的自旋性质。对于整数自旋，如电子的自旋量子数为1/2，称为费米子；对于半整数自旋，如质子的自旋量子数为1/2，称为玻色子。

自旋态的表示

自旋态是描述自旋系统状态的量子态，可以用自旋量子数和自旋角动量投影来表示。自旋角动量投影是自旋角动量在某一方向上的分量，用符号m表示。对于自旋量子数为s的粒子，其自旋态可以表示为|s, m>，其中|s, m>表示自旋量子数为s，自旋角动量投影为m的自旋态。

自旋系统的相互作用

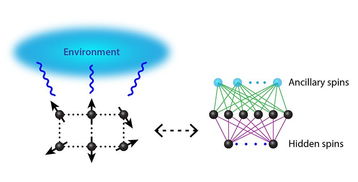
自旋系统中的粒子之间可以存在相互作用，这种相互作用可以是交换力、库仑力或其他类型的力。自旋系统的相互作用可以通过哈密顿量来描述，哈密顿量是量子力学中描述系统总能量的算符。在自旋系统中，哈密顿量通常包含自旋-自旋相互作用项和自旋-轨道相互作用项。

自旋系统的物理应用

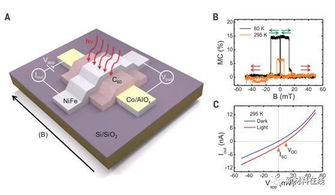
自旋系统在物理学和材料科学中有着广泛的应用。例如，在核磁共振（NMR）技术中，自旋系统被用来研究分子的结构和动态特性。在半导体物理中，自旋系统与电子的能带结构密切相关，对理解电子输运和磁性材料具有重要意义。此外，自旋系统在量子计算和量子信息领域也扮演着关键角色。

自旋系统的数学描述

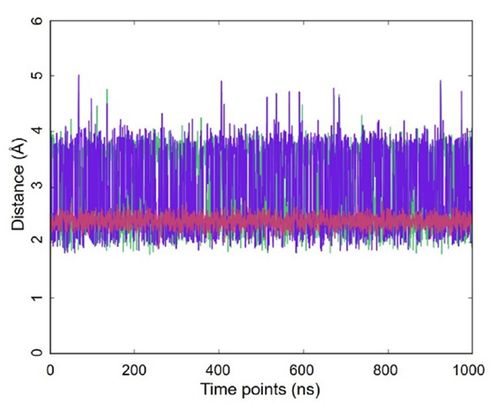
自旋系统的数学描述主要基于量子力学的基本原理。在量子力学中，自旋系统可以用薛定谔方程来描述，薛定谔方程是一个二阶偏微分方程，描述了量子态随时间的演化。对于自旋系统，薛定谔方程可以转化为自旋算符的形式，这些自旋算符满足特定的对易关系，从而描述了自旋系统的物理性质。

自旋系统的实验研究

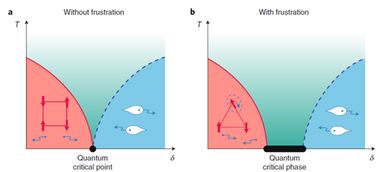
自旋系统的实验研究主要依赖于核磁共振、顺磁共振等实验技术。通过测量自旋系统的磁共振信号，可以获取关于自旋系统性质的信息，如自旋量子数、自旋态、相互作用等。这些实验技术为自旋系统的研究提供了强有力的工具。

自旋系统的未来展望

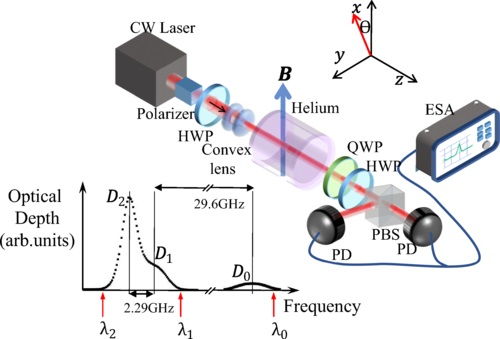
随着量子力学和材料科学的不断发展，自旋系统的研究将继续深入。未来，自旋系统的研究将更加关注以下几个方面：一是探索新的自旋系统材料，以开发新型量子器件；二是研究自旋系统的量子信息应用，如量子计算、量子通信等；三是揭示自旋系统与宏观物理现象之间的关系，为理解复杂系统提供新的视角。

通过以上内容，我们可以看到自旋系统在物理学和材料科学中的重要地位，以及其在实验研究和未来应用中的广阔前景。随着科学技术的不断进步，自旋系统的研究将不断取得新的突破，为人类社会的发展做出更大的贡献。