非线性系统相平面法,揭示动力学行为的二维图解分析

你知道吗？在复杂的科学世界里，有一种方法能让我们像侦探一样，揭开非线性系统的神秘面纱。它就是相平面法！想象你手中有一张地图，上面记录了系统状态的变化轨迹，是不是瞬间觉得科学也变得有趣起来呢？接下来，就让我带你一起探索这个奇妙的世界吧！

一、相平面法的奥秘

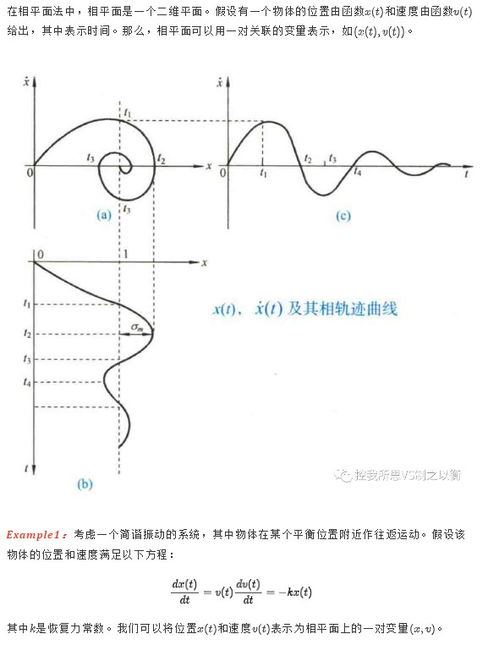
相平面法，顾名思义，就是将系统的状态变量绘制在一个二维平面上。在这个平面上，横坐标代表一个状态变量，纵坐标代表其导数。这样一来，系统的状态变化轨迹就变成了一个曲线，我们称之为相轨迹。

二、相平面法的魅力

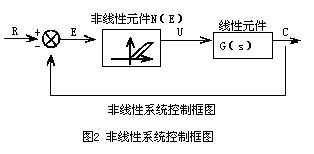
1. 直观易懂：相平面法将复杂的非线性系统简化为二维图形，让我们可以直观地观察到系统的动态行为。

2. 稳定性分析：通过分析相轨迹的形状和特点，我们可以判断系统的稳定性。比如，平衡点、极限环等，都是系统稳定性的重要标志。

3. 周期性分析：相平面法可以帮助我们分析系统的周期性。比如，一个周期性的系统，其相轨迹会呈现出封闭的曲线。

4. 混沌现象：相平面法还可以揭示非线性系统的混沌现象。混沌现象是自然界中普遍存在的现象，如天气变化、股票市场等。

三、相平面法的应用

1. 机械系统：相平面法可以用来分析机械系统的运动规律，如振动、旋转等。

2. 生物系统：相平面法可以用来研究生物系统的动态行为，如心脏跳动、细胞分裂等。

3. 控制系统：相平面法可以用来分析控制系统的稳定性，如PID控制器、模糊控制器等。

四、相平面法的绘制

1. 解析法：通过解析求解微分方程，得到相轨迹的表达式。

2. 数值法：使用数值方法（如Runge-Kutta法）求解微分方程，得到相轨迹。

3. 等倾线法：在相平面上绘制等倾线，即斜率相同的线。相轨迹与等倾线的交点，就是系统的状态变化点。

五、相平面法的局限性

1. 适用范围：相平面法仅适用于一阶和二阶系统。

2. 解析难度：对于复杂的非线性系统，解析求解微分方程可能非常困难。

3. 数值误差：数值方法求解微分方程时，可能会产生误差。

相平面法是一种强大的工具，可以帮助我们更好地理解非线性系统的动态行为。虽然它存在一些局限性，但仍然在各个领域发挥着重要作用。让我们一起探索这个奇妙的世界，揭开非线性系统的神秘面纱吧！