计算器安卓版

标准差计算器的使用与重要性

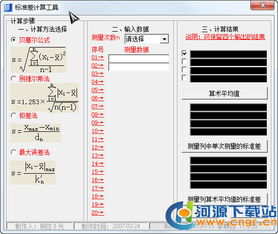
在统计学和数据科学领域，标准差是一个非常重要的概念。它能够帮助我们了解数据集的离散程度，即数据点相对于平均值的分散情况。为了方便计算和快速得到标准差，标准差计算器应运而生。本文将详细介绍标准差计算器的使用方法及其重要性。

标准差（Standard Deviation），通常用符号σ表示，是衡量一组数据离散程度的统计量。它反映了数据点与平均值的平均偏差。标准差越大，说明数据点之间的差异越大；标准差越小，说明数据点之间的差异越小。

标准差的计算公式如下：

\\[ \\sigma = \\sqrt{\\frac{\\sum_{i=1}^{n}(x_i - \\bar{x})^2}{n}} \\]

其中，\\( x_i \\) 表示第 \\( i \\) 个数据点，\\( \\bar{x} \\) 表示所有数据点的平均值，\\( n \\) 表示数据点的数量。

标准差计算器是一种方便快捷的计算工具，可以帮助我们快速得到标准差。以下是使用标准差计算器的步骤：

输入数据：将需要计算标准差的数据输入到计算器中。

计算平均值：计算器会自动计算所有数据点的平均值。

计算偏差：计算器会计算每个数据点与平均值的偏差。

计算平方和：计算器会计算所有偏差的平方和。

计算平均值：计算器会计算偏差平方和的平均值。

开平方：计算器会对平均值开平方，得到标准差。

使用标准差计算器具有以下优势：

提高效率：手动计算标准差需要一定的计算能力，而标准差计算器可以快速得到结果，提高工作效率。

减少错误：手动计算标准差容易出错，而标准差计算器可以减少计算过程中的错误。

方便快捷：标准差计算器操作简单，易于上手。

标准差计算器在以下场景中具有广泛的应用：

统计学：在统计学研究中，标准差是衡量数据离散程度的重要指标。

数据分析：在数据分析过程中，标准差可以帮助我们了解数据的波动情况。

质量控制：在质量控制过程中，标准差可以用来评估产品质量的稳定性。

金融领域：在金融领域，标准差可以用来衡量投资组合的风险。

在使用标准差计算器时，需要注意以下几点：

数据类型：确保输入的数据类型正确，例如，输入的数据应为数值型。

数据量：对于大量数据，使用标准差计算器可以节省时间。

精度：根据实际需求，选择合适的计算精度。

标准差计算器是一种方便快捷的工具，可以帮助我们快速得到标准差。了解标准差及其计算方法对于统计学、数据分析等领域具有重要意义。通过本文的介绍，相信大家对标准差计算器有了更深入的了解。