给定系统微分方程,深入解析给定系统微分方程的求解与应用

深入解析给定系统微分方程的求解与应用

在科学研究和工程实践中，微分方程是描述系统动态行为的重要数学工具。本文将深入探讨给定系统微分方程的求解方法及其在实际应用中的重要性。

微分方程的基本概念与类型

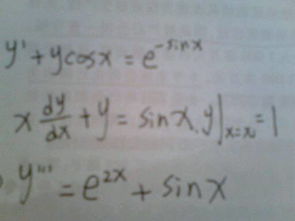
微分方程是描述变量及其导数之间关系的方程。根据方程中导数的阶数，微分方程可以分为一阶微分方程、二阶微分方程等。根据方程的线性或非线性，微分方程又可以分为线性微分方程和非线性微分方程。

给定系统微分方程的求解方法

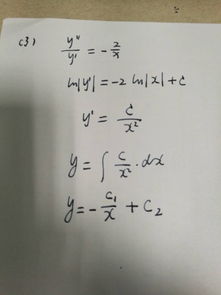
1. 常微分方程的求解方法

常微分方程的求解方法包括分离变量法、积分因子法、常数变易法、特征方程法等。这些方法适用于不同类型的常微分方程，如一阶线性微分方程、二阶常系数线性微分方程等。

2. 偏微分方程的求解方法

偏微分方程的求解方法包括分离变量法、特征值问题法、格林函数法等。这些方法适用于不同类型的偏微分方程，如波动方程、热传导方程等。

微分方程的数值解法

1. 欧拉法

欧拉法是一种简单的数值解法，适用于一阶微分方程。该方法通过迭代计算近似解，但精度较低。

2. 龙格-库塔法

龙格-库塔法是一种更精确的数值解法，适用于一阶和二阶微分方程。该方法通过组合多个欧拉法迭代，提高解的精度。

3. 雅可比矩阵法

雅可比矩阵法是一种基于矩阵运算的数值解法，适用于非线性微分方程。该方法通过求解线性化方程组来近似原方程的解。

微分方程在实际应用中的重要性

1. 物理学

在物理学中，微分方程用于描述物体的运动、热传导、电磁场等现象。例如，牛顿第二定律可以用一阶微分方程表示，而热传导方程可以用偏微分方程表示。

2. 生物学

在生物学中，微分方程用于描述种群动态、细胞信号传导、生物膜电位等过程。例如，Lotka-Volterra方程用于描述捕食者-猎物系统的动态行为。

3. 工程学

在工程学中，微分方程用于设计控制系统、分析电路、优化结构等。例如，传递函数是描述线性系统动态性能的重要数学工具，它基于微分方程建立。

微分方程是描述系统动态行为的重要数学工具，其求解方法多样，应用广泛。本文介绍了微分方程的基本概念、求解方法及其在实际应用中的重要性，旨在为读者提供对该领域的全面了解。