非线性系统化简,非线性系统化简的重要性

非线性系统化简的重要性

非线性系统在工程、物理、生物等多个领域都有广泛的应用。非线性系统的复杂性往往使得分析和设计变得困难。因此，非线性系统化简成为了一个重要的研究课题。通过化简，我们可以降低系统的复杂度，使得分析和设计更加高效和可行。

非线性系统的特点

非线性系统与线性系统相比，具有以下特点：

非线性系统的动态行为复杂，难以用简单的数学模型描述。

非线性系统的稳定性分析困难，可能存在多个稳定状态。

非线性系统的控制设计复杂，需要考虑更多的约束条件。

非线性系统化简的方法

非线性系统化简的方法主要包括以下几种：

线性化方法：在系统的工作点附近，将非线性系统近似为线性系统。这种方法适用于系统工作点附近的动态分析。

状态空间重构：通过引入新的状态变量，将高维非线性系统降维为低维系统。这种方法适用于系统状态空间维度较高的情况。

模型降阶：通过保留系统的主要动态特性，去除不必要的动态特性，降低系统的阶数。这种方法适用于系统阶数较高的情况。

近似方法：使用数学工具（如泰勒展开、保形变换等）对非线性系统进行近似。这种方法适用于系统具有特定类型的非线性特性。

线性化方法的应用

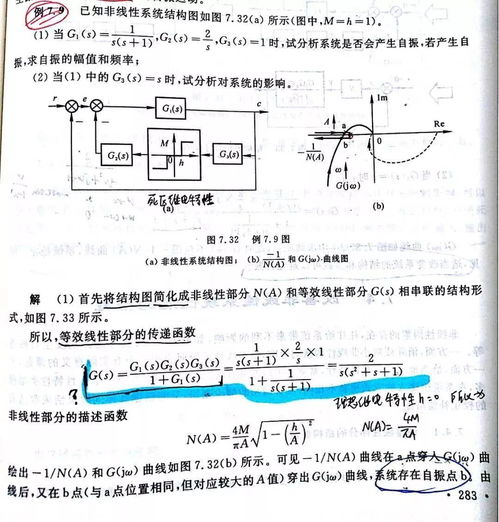
线性化方法是一种常用的非线性系统化简方法。以下是一个线性化方法的例子：

假设有一个非线性系统，其状态方程为：

[ dot{x} = f(x) ]

其中，( f(x) ) 是非线性函数。为了线性化这个系统，我们可以在系统的工作点 ( x_0 ) 处对 ( f(x) ) 进行泰勒展开，保留一阶项，得到线性近似方程：

[ dot{x} approx f'(x_0)(x - x_0) ]

这样，我们就将原来的非线性系统化简为一个线性系统。

状态空间重构的应用

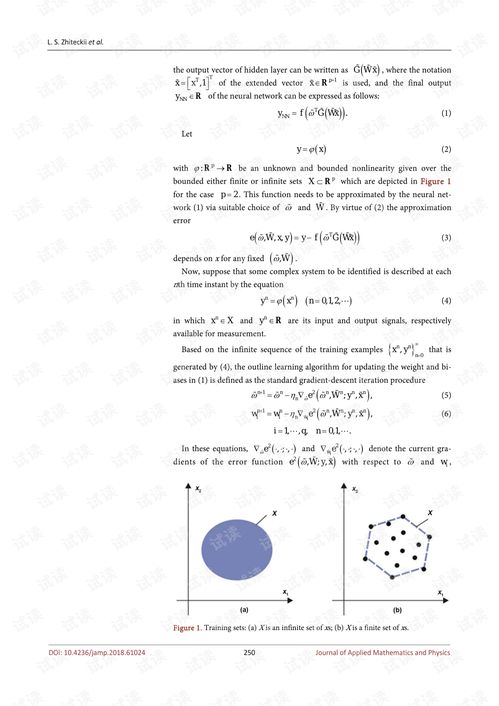
状态空间重构方法通过引入新的状态变量来降低系统的维度。以下是一个状态空间重构的例子：

考虑一个二维非线性系统：

[ dot{x}_1 = f_1(x_1, x_2) ]

[ dot{x}_2 = f_2(x_1, x_2) ]

我们可以通过引入新的状态变量 ( y_1 ) 和 ( y_2 ) 来重构状态空间，使得新的状态方程变为线性形式：

[ dot{y}_1 = g_1(y_1, y_2) ]

[ dot{y}_2 = g_2(y_1, y_2) ]

其中，( g_1 ) 和 ( g_2 ) 是线性函数。

模型降阶的应用

模型降阶方法通过保留系统的主要动态特性来降低系统的阶数。以下是一个模型降阶的例子：

假设有一个高阶非线性系统，我们可以通过以下步骤进行降阶：

识别系统的主要动态特性。

构建一个低阶模型，保留主要动态特性。

验证低阶模型的有效性。

近似方法的应用

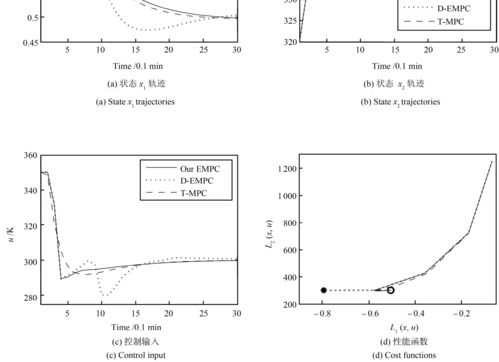
近似方法通过数学工具对非线性系统进行近似。以下是一个近似方法的例子：

考虑一个具有饱和非线性特性的系统，其状态方程为：

[ dot{x} = k(x - x_s) ]

其中，( x_s ) 是饱和函数。我们可以使用保形变换方法对饱和函数进行近似，从而将非线性系统近似为一个线性系统。

非线性系统化简是提高系统分析和设计效率的重要手段。通过线性化、状态空间重构、模型降阶和近似等方法，我们可以有效地降低非线性系统的复杂度，使得系统更加易于分析和控制。在实际应用中，选择合适的化简方法需要根据具体问题进行综合考虑。