非线性系统的分析方法,非线性系统分析方法概述

非线性系统分析方法概述

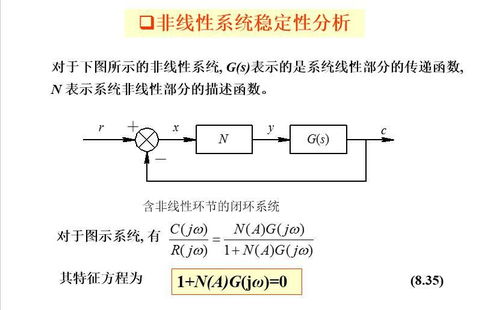
非线性系统在自然界和工程领域中广泛存在，由于其复杂性和非线性行为，对其进行有效的分析和设计一直是控制理论中的一个重要课题。非线性系统的分析方法主要包括时域分析、频域分析、稳定性分析以及数值模拟等。以下将详细介绍这些分析方法。

时域分析方法

时域分析方法是最直观的非线性系统分析方法，它直接在时间域内对系统进行描述和分析。这种方法主要依赖于微分方程或差分方程来描述系统的动态行为。常见的时域分析方法包括以下几种：

数值解法：如欧拉法、龙格-库塔法等，通过离散化时间步长来近似求解微分方程。

解析解法：对于一些简单的非线性系统，可以通过解析方法得到精确的解，如李雅普诺夫函数法、相平面法等。

稳定性分析：通过分析系统在初始扰动下的行为，判断系统是否稳定。常见的稳定性分析方法包括李雅普诺夫稳定性理论和线性化方法。

频域分析方法

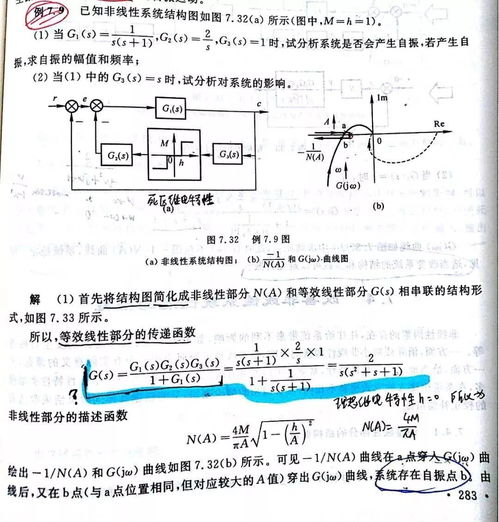
频域分析方法将系统在频域内进行描述和分析，主要利用傅里叶变换将时域信号转换为频域信号。这种方法可以揭示系统在不同频率下的响应特性。常见的频域分析方法包括以下几种：

频谱分析：通过傅里叶变换将时域信号转换为频域信号，分析信号的频率成分。

传递函数分析：通过传递函数描述系统在不同频率下的响应特性，分析系统的稳定性、稳态误差和动态性能。

频率响应分析：通过频率响应函数描述系统在不同频率下的增益、相位和群延迟等特性。

稳定性分析方法

稳定性分析是研究非线性系统在初始扰动下是否能够恢复到平衡状态的重要方法。常见的稳定性分析方法包括以下几种：

李雅普诺夫稳定性理论：通过构造李雅普诺夫函数，分析系统在初始扰动下的行为，判断系统是否稳定。

线性化方法：将非线性系统在平衡点附近线性化，分析线性化系统的稳定性，从而推断原非线性系统的稳定性。

数值稳定性分析：通过数值模拟方法，分析系统在不同初始条件下的行为，判断系统是否稳定。

数值模拟方法

数值模拟方法是通过计算机模拟来研究非线性系统的动态行为。这种方法可以处理复杂的非线性系统，并且可以方便地改变系统参数，研究系统在不同参数下的行为。常见的数值模拟方法包括以下几种：

欧拉法：通过离散化时间步长，近似求解微分方程。

龙格-库塔法：一种更精确的数值解法，适用于求解非线性微分方程。

蒙特卡洛模拟：通过随机抽样来模拟非线性系统的行为，适用于处理具有随机性的非线性系统。

非线性系统的分析方法多种多样，针对不同的系统特性和研究目的，可以选择合适的方法进行分析。在实际应用中，往往需要结合多种方法来全面地研究非线性系统。随着计算机技术的不断发展，数值模拟方法在非线性系统分析中的应用越来越广泛，为非线性系统的研究提供了有力的工具。