非最小相位系统的稳定性,非最小相位系统的定义与特性

非最小相位系统的定义与特性

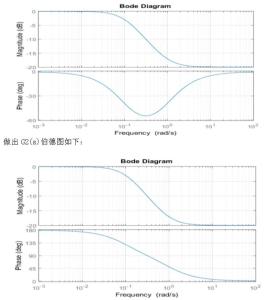
非最小相位系统是指在传递函数的S平面上，至少有一个极点或零点位于右半平面的系统。与最小相位系统相比，非最小相位系统的特性更为复杂，其幅频特性和相频特性之间没有一一对应的关系。

非最小相位系统对系统性能的影响

非最小相位系统对系统性能的影响主要体现在以下几个方面：

稳定性：非最小相位系统可能存在稳定性问题。由于系统在S平面的右半平面存在极点或零点，可能导致系统在特定条件下不稳定。

响应速度：非最小相位系统可能存在响应速度慢的问题。由于系统在S平面的右半平面存在极点或零点，可能导致系统在响应过程中出现相位滞后，从而影响系统的响应速度。

准确性：非最小相位系统可能存在准确性问题。由于系统在S平面的右半平面存在极点或零点，可能导致系统在响应过程中出现幅值变化，从而影响系统的准确性。

非最小相位系统的稳定性分析

非最小相位系统的稳定性分析主要包括以下两个方面：

奈奎斯特判据：奈奎斯特判据是一种常用的稳定性分析方法。对于非最小相位系统，在使用奈奎斯特判据时，需要注意以下几点：

绘制奈奎斯特图时，起点和终点需要根据传递函数进行计算。

求解奈奎斯特图与负实轴的交点时，需要结合传递函数分析相角。

应用Z、P、N关系时，需要考虑开环不稳定极点数P。

根轨迹法：根轨迹法是一种常用的稳定性分析方法。对于非最小相位系统，在使用根轨迹法时，需要注意以下几点：

绘制根轨迹图时，需要考虑传递函数的极点和零点。

分析根轨迹图时，需要关注系统在S平面的右半平面是否存在极点或零点。

非最小相位系统的设计方法

为了提高非最小相位系统的性能，可以采取以下设计方法：

系统降阶：通过降阶处理，可以简化系统结构，提高系统性能。

控制器设计：采用合适的控制器设计方法，如PID控制器、模糊控制器等，可以提高系统的稳定性和响应速度。

滤波器设计：通过设计合适的滤波器，可以抑制系统中的噪声和干扰，提高系统的准确性。

结论

非最小相位系统在工程应用中较为常见，其稳定性分析、设计方法等方面具有一定的挑战性。通过对非最小相位系统的深入研究，可以更好地理解和应用这类系统，提高系统的性能和可靠性。

非最小相位系统 稳定性分析 系统性能 奈奎斯特判据 根轨迹法 控制器设计 滤波器设计