非厄密系统,非厄密系统的探索与挑战

非厄密系统的探索与挑战

在数学和物理学的领域中，厄密系统是一个重要的概念，它描述了一类具有特定对称性的物理系统。非厄密系统在现实世界中同样普遍存在，它们为科学研究和技术应用带来了新的挑战和机遇。本文将探讨非厄密系统的特性、研究方法以及在实际应用中的重要性。

一、非厄密系统的定义与特性

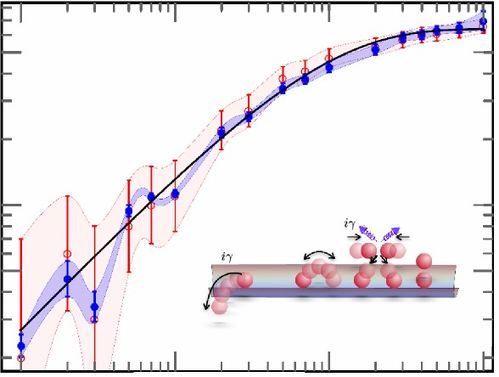
非厄密系统是指那些不具有厄密对称性的物理系统。与厄密系统相比，非厄密系统通常具有以下特性：

非守恒量：非厄密系统中的某些物理量可能不是守恒的，这意味着它们在系统演化过程中会发生变化。

非周期性：非厄密系统的演化可能不是周期性的，即系统不会回到初始状态。

非稳定性：非厄密系统可能更容易受到外部干扰，导致系统状态的不稳定性。

二、非厄密系统的研究方法

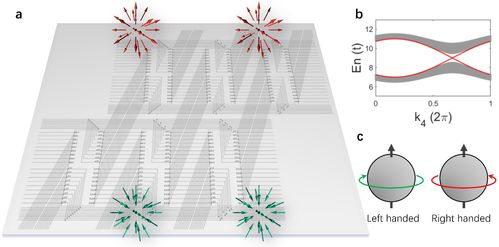
数值模拟：通过计算机模拟非厄密系统的演化过程，可以直观地了解系统的行为和特性。

实验研究：在实验室条件下，通过实验手段研究非厄密系统的行为，有助于揭示其内在规律。

理论分析：基于数学和物理理论，对非厄密系统进行理论分析，有助于揭示其演化规律。

三、非厄密系统在实际应用中的重要性

金融市场：金融市场中的股票、期货等金融产品往往具有非厄密特性，研究这些产品的演化规律有助于投资者做出更明智的投资决策。

生物系统：生物系统中的许多过程，如细胞分裂、种群演化等，都表现出非厄密特性。研究这些过程有助于揭示生物系统的演化规律。

交通系统：交通系统中的车辆流动、交通拥堵等现象也具有非厄密特性。研究这些现象有助于优化交通管理，提高交通效率。

四、非厄密系统研究的未来展望

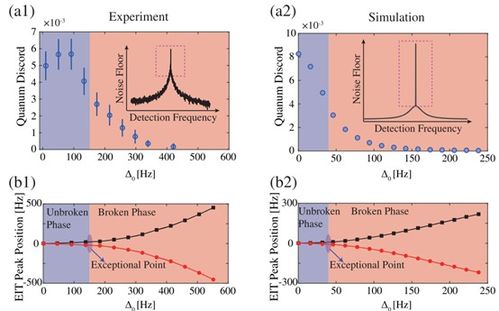
随着科学技术的不断发展，非厄密系统的研究将面临以下挑战和机遇：

跨学科研究：非厄密系统研究需要数学、物理、生物学、经济学等多个学科的交叉融合。

大数据分析：利用大数据技术，可以更全面地研究非厄密系统的演化规律。

人工智能：人工智能技术可以应用于非厄密系统的模拟和预测，提高研究效率。

非厄密系统在现实世界中具有广泛的应用，研究这类系统对于揭示自然规律、优化技术应用具有重要意义。随着科学技术的不断发展，非厄密系统研究将面临新的挑战和机遇，为人类社会的进步提供更多可能性。