非线性系统平衡点,非线性系统平衡点的概念与重要性

非线性系统平衡点的概念与重要性

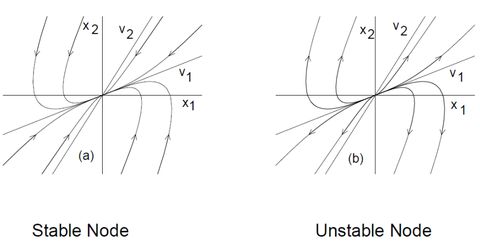
非线性系统在自然界和工程领域中广泛存在，由于其复杂性和非线性行为，对这类系统的分析和控制一直是科学研究的热点。在非线性系统中，平衡点是一个核心概念，它代表了系统在无外力作用下，状态变量保持不变的状态。平衡点的稳定性直接关系到系统的性能和安全性，因此，研究非线性系统平衡点具有重要意义。

平衡点的定义与分类

平衡点是指非线性系统中，所有状态变量随时间变化率为零的状态。在数学上，如果存在一组参数值，使得系统方程的解在该组参数值下不随时间变化，则称这组参数值对应的系统状态为平衡点。根据平衡点的稳定性，可以分为以下几类：

渐近稳定平衡点：系统在平衡点附近，任何微小的扰动都会使系统状态逐渐趋向于平衡点。

稳定平衡点：系统在平衡点附近，任何微小的扰动都会使系统状态趋向于平衡点，但可能存在一定的振荡。

不稳定平衡点：系统在平衡点附近，任何微小的扰动都会使系统状态远离平衡点。

半稳定平衡点：系统在平衡点附近，扰动可能导致系统状态趋向于平衡点或远离平衡点。

平衡点的分析方法

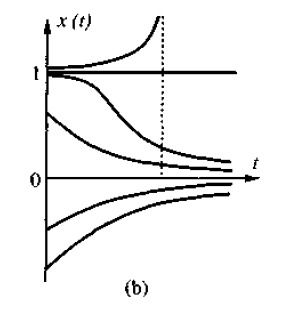
分析非线性系统平衡点的方法主要有以下几种：

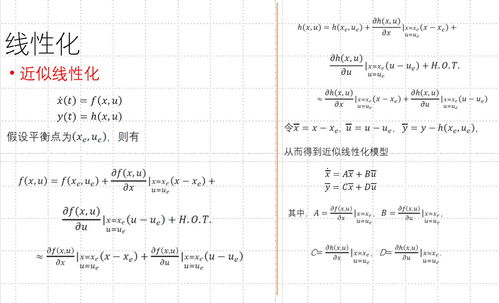
线性化方法：在平衡点附近，将非线性系统近似为线性系统，然后分析线性系统的稳定性。

李雅普诺夫函数方法：构造一个李雅普诺夫函数，通过分析该函数的性质来判断平衡点的稳定性。

数值方法：利用计算机模拟，对非线性系统进行数值求解，观察系统状态的变化趋势。

平衡点在工程中的应用

平衡点在工程中的应用非常广泛，以下列举几个例子：

控制系统设计：在控制系统设计中，平衡点代表了系统的期望状态，通过设计控制器，使系统状态趋向于平衡点。

机器人控制：在机器人控制中，平衡点代表了机器人的稳定状态，通过控制算法，使机器人保持平衡。

电力系统稳定：在电力系统中，平衡点代表了系统的稳定状态，通过控制策略，使系统保持稳定运行。

平衡点研究的挑战与展望

尽管平衡点在理论和工程中具有重要意义，但对其研究仍面临一些挑战：

复杂性：非线性系统往往具有复杂的动力学行为，这使得平衡点的分析变得困难。

不确定性：实际系统中存在各种不确定性因素，这可能导致平衡点的变化。

计算复杂性：平衡点的分析方法往往需要大量的计算资源，这在实际应用中可能成为限制因素。

针对这些挑战，未来平衡点研究可以从以下几个方面进行：

发展新的分析方法：探索更有效的平衡点分析方法，降低计算复杂性。

提高模型精度：通过引入更多参数和变量，提高非线性系统的模型精度。

结合人工智能技术：利用人工智能技术，提高平衡点分析的计算效率和准确性。

非线性系统平衡点的研究对于理解系统行为、设计控制系统以及解决实际问题具有重要意义。尽管目前仍存在一些挑战，但随着理论研究的深入和计算技术的进步，相信平衡点研究将取得更多突破。