非线性系统分析,非线性系统分析概述

非线性系统分析概述

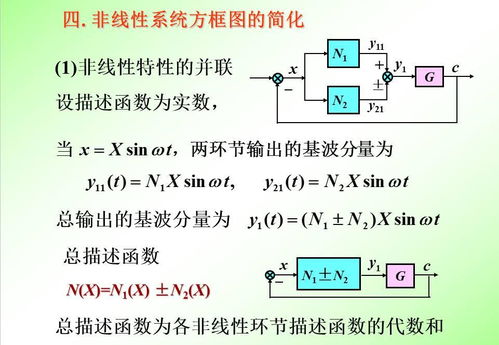
非线性系统分析是现代数学和工程学中的一个重要领域，它涉及对那些行为无法用线性方程描述的系统的研究。非线性系统在自然界和工程实践中广泛存在，如生态系统、金融市场、电子电路等。本文将简要介绍非线性系统分析的基本概念、研究方法及其在各个领域的应用。

非线性系统的基本特性

非线性的动态行为：非线性系统可能表现出复杂的动态行为，如混沌、分岔、极限环等。

非线性系统的稳定性：非线性系统的稳定性分析比线性系统更为复杂，需要考虑系统的全局和局部稳定性。

非线性系统的可控性和可观测性：非线性系统的可控性和可观测性分析是设计控制器和观测器的基础。

非线性系统分析方法

非线性系统分析方法主要包括以下几种：

数值方法：通过计算机模拟来研究非线性系统的行为，如数值积分、数值解法等。

解析方法：通过数学推导和理论分析来研究非线性系统的性质，如李雅普诺夫稳定性理论、分岔理论等。

几何方法：利用相空间和相图来直观地描述非线性系统的动态行为。

非线性系统分析的应用

非线性系统分析在各个领域都有广泛的应用，以下列举几个典型应用领域：

物理学：研究非线性波动方程、混沌现象等。

生物学：研究生态系统、神经元网络等。

工程学：研究非线性控制系统、电子电路等。

经济学：研究金融市场、宏观经济模型等。

非线性系统分析的挑战与展望

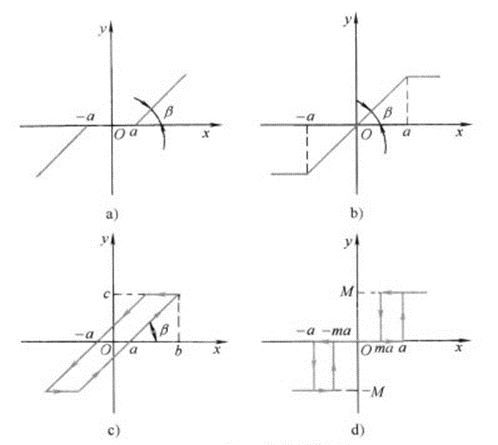
非线性系统分析虽然取得了显著的进展，但仍面临一些挑战：

理论框架的完善：目前非线性系统分析的理论框架还不够完善，需要进一步发展新的理论和方法。

计算方法的改进：随着非线性系统规模的增大，计算方法需要不断改进以提高计算效率和精度。

跨学科研究：非线性系统分析需要与其他学科如物理学、生物学、经济学等进行交叉研究，以解决复杂问题。

展望未来，非线性系统分析将在以下方面取得更多突破：

发展新的理论和方法，以更好地描述和预测非线性系统的行为。

提高计算效率，解决更大规模的非线性系统问题。

促进跨学科研究，推动非线性系统分析在各个领域的应用。

结论

非线性系统分析是一个充满挑战和机遇的领域。通过对非线性系统的研究，我们可以更好地理解自然界和工程实践中的复杂现象，为解决实际问题提供理论和方法支持。随着科学技术的不断发展，非线性系统分析将在未来发挥越来越重要的作用。