分型l系统,分型L系统的概述与重要性

分型L系统的概述与重要性

分型L系统，作为一种在数学、统计学以及工程学等领域广泛应用的工具，其重要性不言而喻。本文将详细介绍分型L系统的概念、特点以及在实际应用中的重要性。

分型L系统的定义与基本原理

分型L系统，全称为分形线性系统，是一种描述非线性动态系统行为的数学模型。它由分形几何和线性系统理论相结合而成，能够有效地描述复杂系统的动态特性。

在分型L系统中，分形几何的概念被用来描述系统状态的演化过程，而线性系统理论则用于分析系统状态之间的转换关系。这种结合使得分型L系统在处理复杂系统时具有独特的优势。

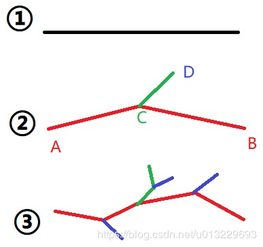
分型L系统的基本原理可以概括为：通过将系统状态空间划分为若干个分形区域，并建立每个区域内的线性映射关系，从而实现对整个系统动态行为的描述。

分型L系统的特点与应用领域

分型L系统具有以下特点：

非线性：能够描述复杂系统的非线性动态行为。

分形：系统状态空间具有分形结构，能够捕捉系统演化的复杂特征。

线性映射：系统状态之间的转换关系可以用线性映射来描述，便于分析和计算。

分型L系统在以下领域具有广泛的应用：

物理学：描述混沌现象、非线性动力学等。

生物学：研究生物种群动态、神经网络等。

经济学：分析金融市场、经济波动等。

工程学：优化控制系统、预测系统行为等。

分型L系统的建模与仿真

分型L系统的建模与仿真主要包括以下步骤：

确定系统状态空间：根据实际问题，确定系统状态空间及其分形结构。

建立线性映射：根据系统状态之间的转换关系，建立线性映射模型。

仿真实验：利用计算机软件对分型L系统进行仿真实验，分析系统动态行为。

结果分析：对仿真结果进行分析，验证模型的有效性，并进一步优化模型。

在实际应用中，分型L系统的建模与仿真需要结合具体问题，灵活运用数学工具和计算机技术。

分型L系统的发展趋势与挑战

随着科学技术的不断发展，分型L系统在理论研究和实际应用方面都取得了显著成果。未来，分型L系统的发展趋势主要包括：

理论创新：深入研究分形几何与线性系统理论的结合，拓展分型L系统的应用范围。

算法优化：提高分型L系统建模与仿真的计算效率，降低计算复杂度。

跨学科应用：与其他学科领域相结合，解决更多实际问题。

分型L系统在发展过程中也面临着一些挑战，如理论体系的完善、算法的优化以及跨学科应用的拓展等。

分型L系统作为一种描述非线性动态系统行为的数学模型，具有广泛的应用前景。通过对分型L系统的深入研究，有助于我们更好地理解复杂系统的动态特性，为解决实际问题提供有力工具。

随着科学技术的不断发展，分型L系统将在理论研究和实际应用方面取得更多突破，为人类社会的发展做出更大贡献。