高阶系统的瞬态响应,高阶系统的瞬态响应概述

高阶系统的瞬态响应概述

在自动控制系统中，高阶系统是指具有三个或更多独立能控或能观状态的系统。这类系统在工程应用中十分常见，如复杂的机械系统、化工过程控制等。高阶系统的瞬态响应分析是控制系统设计中的重要环节，它直接关系到系统的稳定性和性能指标。

高阶系统瞬态响应的特点

高阶系统的瞬态响应具有以下特点：

响应复杂：高阶系统的响应曲线通常较为复杂，可能包含多个振荡周期，甚至出现混沌现象。

响应速度慢：由于系统阶数较高，响应速度相对较慢，需要较长时间才能达到稳态。

稳定性难以保证：高阶系统的稳定性分析较为复杂，需要综合考虑各种因素，如极点分布、零点分布等。

高阶系统瞬态响应分析方法

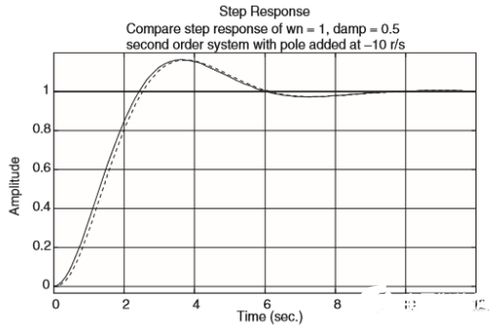
高阶系统瞬态响应分析方法主要包括以下几种：

直接求解法：通过求解高阶微分方程，得到系统瞬态响应的表达式。

间接评价法：利用系统传递函数或状态空间表达式，通过计算系统性能指标来评价瞬态响应。

计算机仿真法：利用计算机仿真软件，对高阶系统进行仿真实验，分析瞬态响应。

高阶系统瞬态响应性能指标

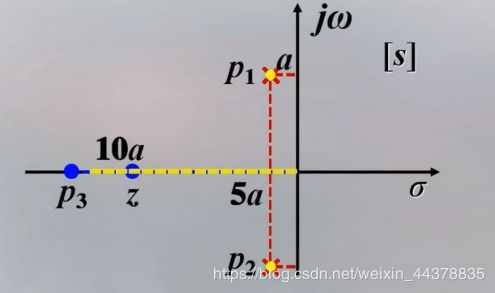
高阶系统瞬态响应性能指标主要包括以下几种：

上升时间（Tr）：系统响应从初始值上升到稳态值所需的时间。

超调量（Ou）：系统响应达到稳态值时，超过稳态值的最大偏差。

调节时间（T90）：系统响应达到并保持在稳态值±2%范围内所需的时间。

稳态误差（Ess）：系统响应达到稳态值时，与期望值的偏差。

高阶系统瞬态响应改善措施

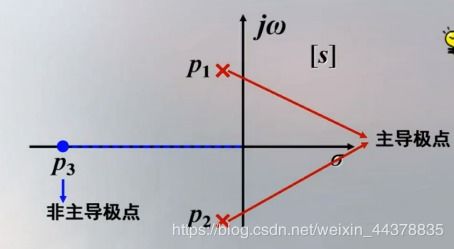
为了改善高阶系统的瞬态响应，可以采取以下措施：

降低系统阶数：通过简化系统模型，降低系统阶数，从而提高响应速度。

调整系统参数：通过调整系统参数，如增益、时间常数等，改变系统响应特性。

引入控制器：通过引入控制器，如PID控制器、模糊控制器等，对系统进行调节，改善瞬态响应。

高阶系统瞬态响应案例分析

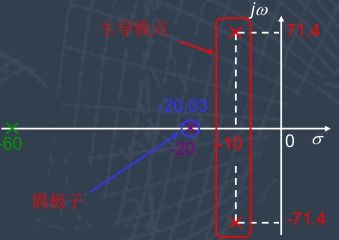
以下是一个高阶系统瞬态响应的案例分析：

假设一个高阶系统，其传递函数为：

G(s) = frac{K}{(s+1)(s^2+2s+2)}

其中，K为系统增益。

通过计算机仿真，可以得到该系统的阶跃响应曲线，如图所示。从图中可以看出，该系统存在两个振荡周期，超调量为30%，调节时间为5秒。