capm 系统性风险,CAPM模型在系统性风险分析中的应用与探讨

CAPM模型在系统性风险分析中的应用与探讨

随着金融市场的发展，系统性风险成为投资者和监管机构关注的焦点。系统性风险是指由于宏观经济、市场结构或政策变化等因素导致的整个金融市场或经济体系的风险。资本资产定价模型（CAPM）作为一种经典的金融理论模型，在系统性风险分析中发挥着重要作用。本文将探讨CAPM模型在系统性风险分析中的应用及其局限性。

一、CAPM模型概述

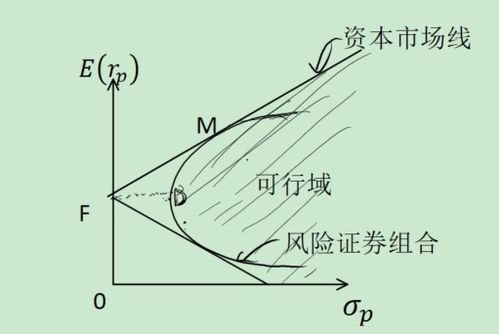
CAPM模型由夏普（Sharpe）、林特纳（Lintner）和莫辛（Mossin）在20世纪60年代提出，是现代金融理论的重要组成部分。该模型认为，资产的预期收益率与其风险之间存在线性关系，即资产的预期收益率等于无风险收益率加上风险溢价。CAPM模型的核心公式为：E(Ri) = Rf + βi (E(Rm) - Rf)，其中E(Ri)表示资产i的预期收益率，Rf表示无风险收益率，βi表示资产i的贝塔系数，E(Rm)表示市场组合的预期收益率。

二、CAPM模型在系统性风险分析中的应用

1. 评估资产风险：CAPM模型通过计算资产的贝塔系数，可以评估资产的风险水平。贝塔系数越高，表示资产的风险越大。在系统性风险分析中，投资者可以利用CAPM模型评估不同资产的风险，从而进行风险管理和投资决策。

2. 评估市场风险溢价：CAPM模型可以计算市场风险溢价，即市场组合的预期收益率与无风险收益率之差。市场风险溢价反映了市场整体风险水平，对于投资者而言，了解市场风险溢价有助于判断投资机会和风险承受能力。

3. 评估投资组合风险：CAPM模型可以计算投资组合的贝塔系数，从而评估投资组合的风险水平。投资者可以根据投资组合的贝塔系数，调整投资策略，降低系统性风险。

4. 评估政策变化对市场的影响：CAPM模型可以用于分析政策变化对市场的影响。例如，当政府实施宽松的货币政策时，市场风险溢价可能会下降，从而降低系统性风险。

三、CAPM模型的局限性

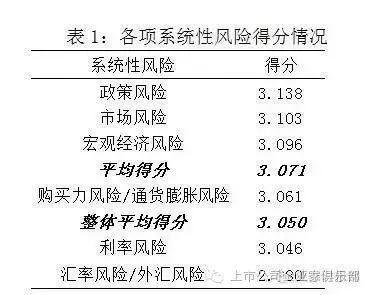
1. 市场有效性假设：CAPM模型基于市场有效性的假设，即市场信息充分、价格合理。然而，现实市场中存在信息不对称、市场操纵等问题，导致市场有效性难以实现。

2. 贝塔系数的估计：CAPM模型中的贝塔系数需要通过历史数据进行估计，而历史数据可能无法完全反映未来市场情况。此外，贝塔系数的估计方法也存在一定的主观性。

3. 无风险收益率的确定：CAPM模型中的无风险收益率需要选取一个合适的基准，而不同投资者对无风险收益率的选取可能存在差异。

4. 模型适用范围：CAPM模型主要适用于股票市场，对于其他金融工具（如债券、衍生品等）的适用性有限。

四、结论

CAPM模型在系统性风险分析中具有一定的应用价值，但同时也存在局限性。投资者和监管机构在应用CAPM模型时，应充分了解其优缺点，并结合实际情况进行风险管理和决策。未来，随着金融理论的不断发展和市场环境的不断变化，CAPM模型将不断完善，为系统性风险分析提供更有效的工具。