dft三大系统,解析、应用与未来展望

DFT三大系统：解析、应用与未来展望

数字信号处理（Digital Signal Processing，DSP）是现代电子技术中不可或缺的一部分，而离散傅里叶变换（Discrete Fourier Transform，DFT）作为其核心算法之一，在信号处理领域扮演着至关重要的角色。本文将深入探讨DFT的三大系统，分析其原理、应用以及未来发展趋势。

一、DFT系统概述

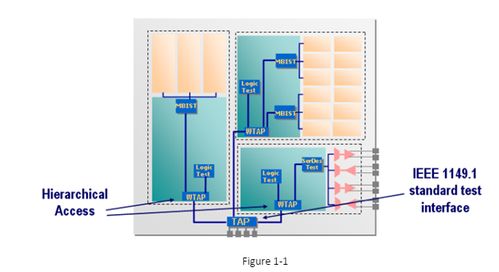
DFT是一种将离散时间信号转换为频域信号的方法，它将时域信号分解为不同频率的正弦波和余弦波的线性组合。DFT系统主要包括以下三个部分：

时域信号：原始信号在时间轴上的表示。

频域信号：时域信号经过DFT变换后的结果，表示信号在不同频率上的分布。

DFT算法：实现时域信号到频域信号转换的计算方法。

二、DFT系统的原理

DFT的原理基于傅里叶级数，将时域信号分解为不同频率的正弦波和余弦波。具体来说，DFT将一个N点序列的时域信号转换为N点序列的频域信号，其计算公式如下：

$$X[k] = sum_{n=0}^{N-1} x[n] cdot e^{-j2pi kn/N}$$

其中，$X[k]$表示频域信号，$x[n]$表示时域信号，$N$表示序列长度，$k$表示频率索引。

三、DFT系统的应用

DFT在各个领域都有广泛的应用，以下列举几个典型应用场景：

通信系统：DFT在通信系统中用于信号调制、解调、滤波等，提高信号传输质量。

图像处理：DFT在图像处理中用于图像压缩、去噪、边缘检测等，提高图像质量。

音频处理：DFT在音频处理中用于音频信号分析、合成、滤波等，改善音频效果。

生物医学：DFT在生物医学领域用于心电图、脑电图等信号分析，辅助疾病诊断。

四、DFT系统的未来展望

算法优化：针对DFT算法进行优化，提高计算效率，降低资源消耗。

硬件实现：利用专用硬件加速DFT计算，提高处理速度。

应用拓展：将DFT系统应用于更多领域，如物联网、人工智能等。

跨学科融合：将DFT与其他学科相结合，如量子计算、生物信息学等，拓展DFT的应用范围。