1阶系统,什么是一阶系统什么是二阶系统

一阶系统的概述

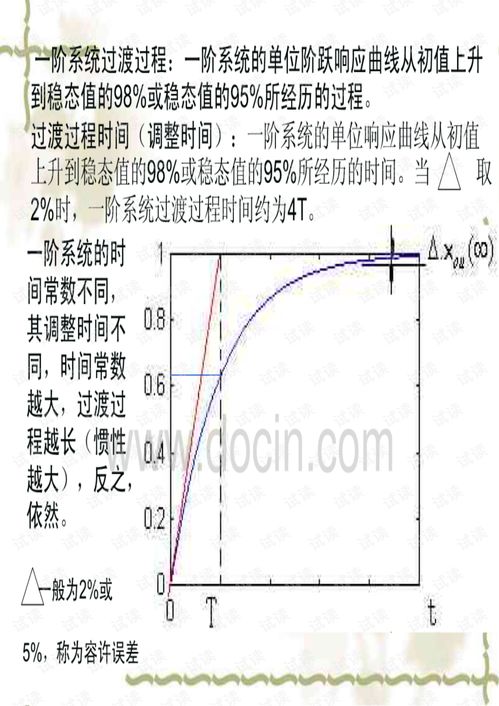
一阶系统是自动控制理论中的一个基本概念，它指的是那些可以用一阶微分方程描述的系统。这类系统在工程和科学研究中非常常见，因为许多实际系统都可以简化为一阶模型。一阶系统通常具有简单的动态特性，便于分析和设计。

一阶系统的数学模型

一阶系统的数学模型通常由一阶线性微分方程给出。最常见的一阶系统模型是RC电路和RL电路。以RC电路为例，其微分方程可以表示为：( frac{dq}{dt} + frac{q}{RC} = 0 )，其中q是电容上的电荷，t是时间，R是电阻，C是电容。这个方程描述了电容充电或放电的过程。

一阶系统的传递函数

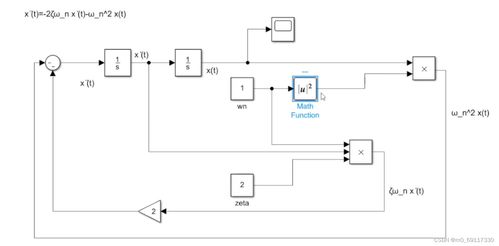
传递函数是系统分析中的一个重要工具，它将系统的输入和输出联系起来。对于一阶系统，其传递函数可以表示为：( H(s) = frac{a}{s} )，其中a是系统常数，s是拉普拉斯变换中的复变量。传递函数提供了系统在频域内的动态特性，有助于分析系统的稳定性、响应速度等性能指标。

一阶系统的时域响应

时域响应是指系统对输入信号的直接响应。对于一阶系统，其时域响应可以通过求解微分方程得到。以RC电路为例，当电容从初始状态开始充电时，其电压v(t)随时间的变化可以表示为：( v(t) = frac{U}{1 + frac{t}{RC}} )，其中U是电源电压。这个公式描述了电容电压随时间逐渐接近稳态电压的过程。

一阶系统的阶跃响应

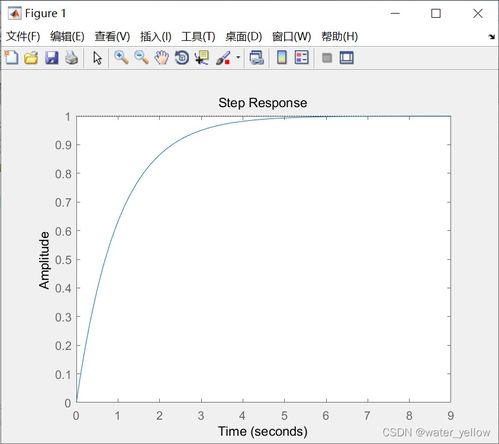
阶跃响应是系统对阶跃输入信号的响应。对于一阶系统，阶跃响应通常表现为指数衰减的形式。以RC电路为例，当电容从初始状态开始充电时，其电压v(t)的阶跃响应可以表示为：( v(t) = U(1 - e^{-frac{t}{RC}}) )。这个公式描述了电容电压在阶跃输入后逐渐接近稳态电压的过程，其中e是自然对数的底数。

一阶系统的性能指标

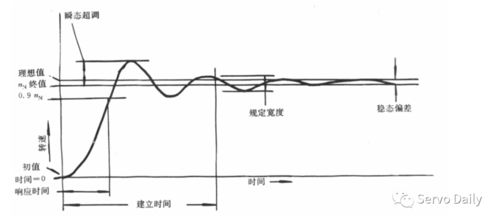
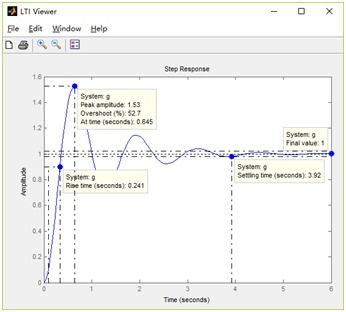
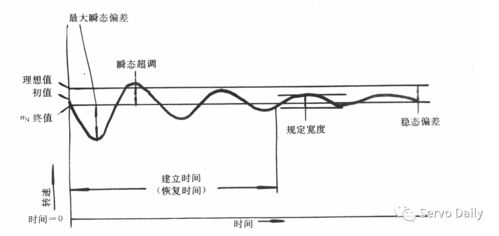
一阶系统的性能指标主要包括动态性能指标和稳态性能指标。动态性能指标描述了系统响应的快慢，如上升时间、峰值时间、调节时间等。稳态性能指标描述了系统在稳态下的性能，如稳态误差、稳态增益等。通过分析这些性能指标，可以评估一阶系统的优劣，并对其进行优化设计。

一阶系统的应用

一阶系统在工程和科学研究中有着广泛的应用。例如，在电子工程中，RC电路和RL电路被广泛应用于滤波、放大、振荡等领域。在生物医学工程中，一阶系统模型可以用于描述药物在体内的代谢过程。在控制工程中，一阶系统模型可以用于分析和设计控制系统，如PID控制器等。

一阶系统是自动控制理论中的一个基本概念，具有简单的动态特性和易于分析的数学模型。通过对一阶系统的深入研究，可以更好地理解和设计实际工程中的系统。随着科学技术的不断发展，一阶系统模型在各个领域的应用将越来越广泛。