2阶系统,什么是2阶系统？

什么是2阶系统？

在控制理论中，2阶系统是指具有两个独立能控或能观状态变量的线性时不变系统。这类系统在工程实践中非常常见，如电机控制、伺服系统等。2阶系统的特点是具有两个自由度，可以通过调整系统的参数来控制系统的动态响应。

2阶系统的数学模型

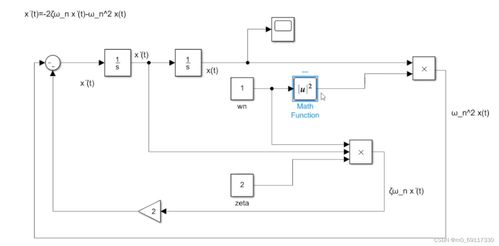
2阶系统的数学模型通常用二阶常系数线性微分方程来描述。一个典型的2阶系统可以表示为以下形式：

[ ddot{x}(t) + 2zetaomega_ndot{x}(t) + omega_n^2x(t) = u(t) ]

其中，( x(t) ) 是系统的输出，( u(t) ) 是输入，( omega_n ) 是系统的自然频率，( zeta ) 是阻尼比。这个方程的解可以描述系统的动态行为，包括上升时间、超调量、稳态误差等性能指标。

2阶系统的性能指标

2阶系统的性能指标主要包括以下几种：

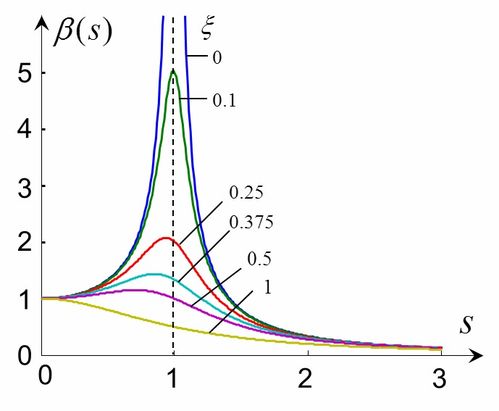
上升时间（( t_r )）：系统从稳态值的10%上升到稳态值的90%所需的时间。

超调量（( M )）：系统响应达到稳态值时的最大偏差与稳态值之比，通常用百分比表示。

稳态误差（( e_{ss} )）：系统在稳态时输出与期望输出之间的误差。

阻尼比（( zeta )）：系统阻尼程度的一个无量纲参数，反映了系统响应的振荡程度。

自然频率（( omega_n )）：系统在没有阻尼时振荡的频率。

2阶系统的稳定性分析

2阶系统的稳定性分析主要依赖于其特征方程的根。特征方程为：

[ r^2 + 2zetaomega_nr + omega_n^2 = 0 ]

根据特征根的实部和虚部，可以判断系统的稳定性。如果特征根的实部为负，则系统是稳定的；如果实部为零，则系统是临界稳定的；如果实部为正，则系统是不稳定的。

2阶系统的控制器设计

为了改善2阶系统的性能，通常需要设计合适的控制器。常见的控制器有比例控制器（P）、积分控制器（I）、微分控制器（D）和比例-积分-微分控制器（PID）。通过调整控制器的参数，可以优化系统的动态响应和稳态性能。

例如，使用PID控制器可以同时调整比例、积分和微分参数，以达到以下目的：

提高系统的响应速度。

减小超调量。

减小稳态误差。

2阶系统的实际应用

电机控制：在工业自动化领域，2阶系统常用于电机控制，以实现精确的位置和速度控制。

伺服系统：在机器人、数控机床等领域，2阶系统用于实现高精度的运动控制。

汽车悬挂系统：2阶系统用于模拟汽车悬挂的动态特性，以优化驾驶舒适性和安全性。

生物医学工程：在医疗设备中，2阶系统用于模拟生物组织的动态响应，以实现精确的治疗。

2阶系统是控制理论中的一个重要概念，它在工程实践中有着广泛的应用。通过对2阶系统的数学模型、性能指标、稳定性分析和控制器设计等方面的研究，可以优化系统的动态响应和稳态性能，从而提高工程系统的可靠性和效率。