823信号与系统,信号与系统的基本概念

信号与系统是电子工程和通信工程领域的基础学科，其中823信号与系统课程是学习信号处理和分析的关键。本文将详细介绍823信号与系统的基本概念、重要理论以及在实际应用中的重要性。

信号与系统的基本概念

信号是信息传递的载体，可以是模拟信号或数字信号。系统则是处理信号的设备或算法，它可以将输入信号转换为输出信号。在823信号与系统中，我们主要研究线性时不变系统（LTI）。

线性时不变系统

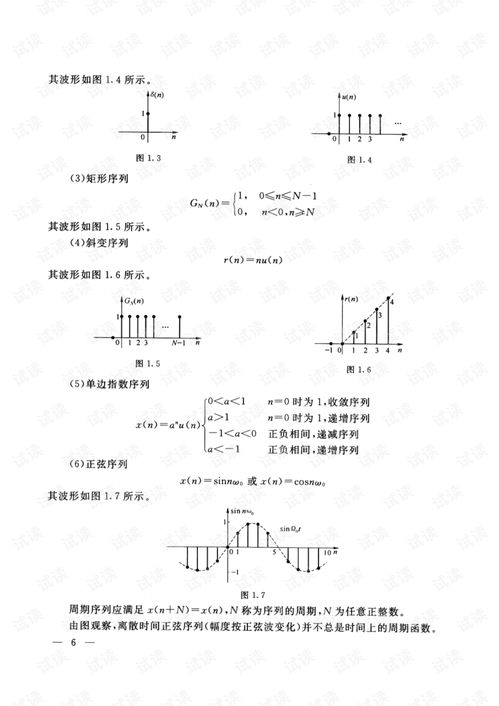
线性时不变系统是信号与系统理论的核心概念之一。线性系统意味着系统的输出是输入信号的线性组合，而时不变系统则意味着系统的特性不随时间变化。线性时不变系统的数学模型通常用差分方程或微分方程表示。

系统分析的方法

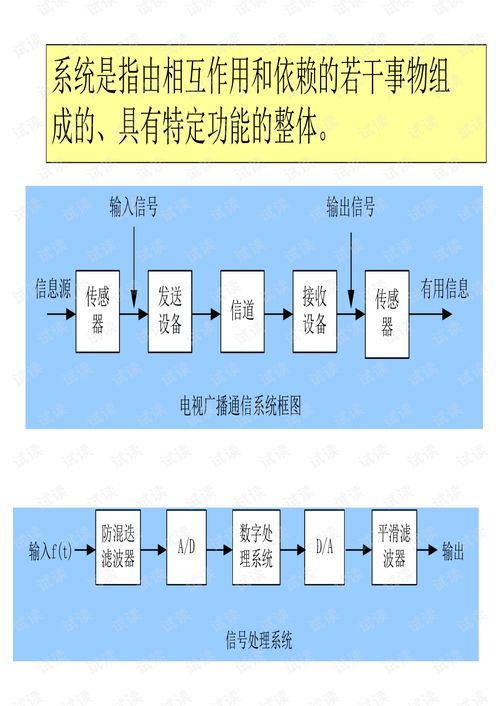
在823信号与系统中，系统分析的方法主要包括时域分析和频域分析。时域分析关注系统对信号的直接响应，而频域分析则关注系统对不同频率信号的响应。

时域分析

时域分析主要包括系统响应的求解和系统特性的分析。系统响应的求解可以通过求解差分方程或微分方程来实现。系统特性的分析包括稳定性分析、因果性分析和线性时不变性分析。

频域分析

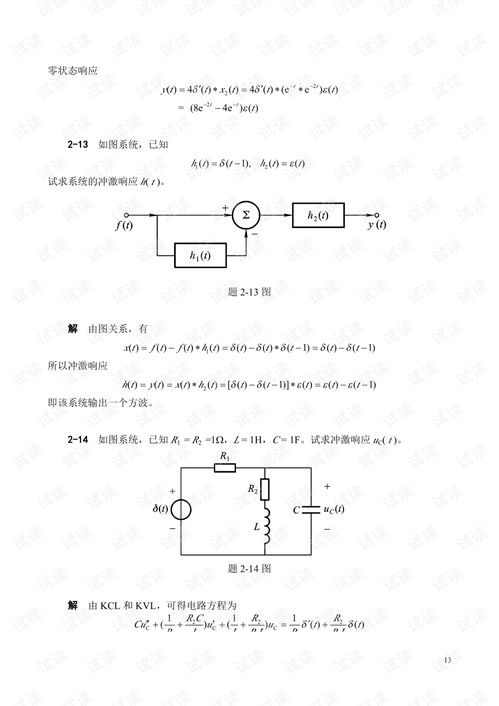
频域分析是信号与系统理论中的重要工具，它可以将时域信号转换为频域信号，从而更容易分析系统的特性。频域分析主要包括傅里叶变换、拉普拉斯变换和Z变换等。

傅里叶变换

傅里叶变换是信号与系统理论中最基本的变换之一，它可以将时域信号转换为频域信号。傅里叶变换具有许多重要的性质，如线性、时移、频移和卷积定理等。

拉普拉斯变换

拉普拉斯变换是傅里叶变换的推广，它适用于分析线性时不变系统。拉普拉斯变换具有许多优点，如可以处理时域信号中的初始条件，并且可以简化系统分析的复杂性。

Z变换

Z变换是离散时间信号与系统理论中的基本变换，它类似于傅里叶变换和拉普拉斯变换。Z变换可以用于分析离散时间系统，并且可以处理系统中的延迟和反馈。

系统设计与应用

823信号与系统的理论在实际应用中具有重要意义。例如，在通信系统中，信号与系统理论用于设计调制解调器、滤波器和信号处理器。在音频处理中，信号与系统理论用于音频信号的压缩、降噪和回声消除。

结论

823信号与系统是电子工程和通信工程领域的基础课程，它涵盖了信号处理和分析的基本理论和方法。通过学习823信号与系统，学生可以掌握信号与系统的基本概念，并能够将其应用于实际问题中。

- 信号与系统

- 线性时不变系统

- 时域分析

- 频域分析

- 傅里叶变换

- 拉普拉斯变换

- Z变换

- 系统设计

- 应用