非线性系统相平面法,非线性系统相平面法在动力学行为分析中的应用

你知道吗？在复杂的科学世界里，有一种方法能让我们像侦探一样，揭开非线性系统的神秘面纱。它就是相平面法！想象你手中有一张神奇的地图，上面记录了系统状态的变化轨迹，是不是很神奇？今天，就让我带你一起探索这个神秘的世界，揭开非线性系统相平面法的神秘面纱吧！

一、什么是非线性系统相平面法？

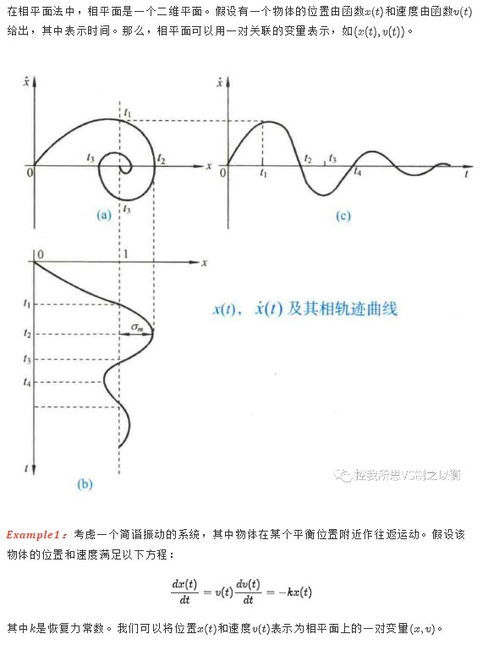
非线性系统，听起来是不是很高端？简单来说，就是那些不按套路出牌的系统。它们的行为复杂多变，让人捉摸不透。而相平面法，就像一把钥匙，能帮助我们打开这扇神秘的大门。

相平面法，顾名思义，就是将系统的状态变量绘制在一个二维平面上，形成一个“相平面”。在这个平面上，你可以看到系统状态随时间变化的轨迹，就像一条条蜿蜒曲折的河流。通过分析这些轨迹，我们就能了解系统的稳定性、周期性、吸引子等特性。

二、相平面法的魅力

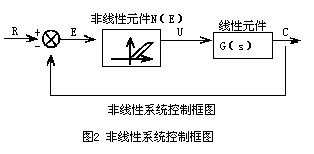
1. 直观易懂：相比复杂的数学公式，相平面法更直观易懂。你只需要一张图，就能一目了然地了解系统的动态行为。

2. 适用范围广：相平面法不仅适用于一阶和二阶系统，还能应用于更复杂的非线性系统。

3. 分析全面：相平面法能帮助我们分析系统的稳定性、周期性、吸引子等特性，为系统设计提供有力支持。

三、如何绘制相平面图？

绘制相平面图，其实就像画一幅画。下面，我就来教你几招：

1. 确定状态变量：首先，你需要确定系统的状态变量。对于一阶系统，通常只需要一个状态变量；对于二阶系统，则需要两个状态变量。

2. 建立微分方程：根据系统的物理模型，建立状态变量的微分方程。

3. 求解微分方程：使用数值方法求解微分方程，得到状态变量随时间的变化规律。

4. 绘制相轨迹：在相平面上，以状态变量为坐标轴，绘制状态变量随时间变化的轨迹。

5. 分析相轨迹：根据相轨迹的形状，分析系统的稳定性、周期性、吸引子等特性。

四、相平面法的应用

相平面法在工程领域有着广泛的应用，比如：

1. 控制系统设计：通过相平面法分析系统的稳定性，为控制系统设计提供依据。

2. 信号处理：在信号处理领域，相平面法可以用于分析信号的频谱特性。

3. 生物系统：在生物系统中，相平面法可以用于研究生物种群的增长规律。

五、相平面法的局限性

虽然相平面法有着诸多优点，但也有一些局限性：

1. 数值方法误差：在求解微分方程时，数值方法可能会引入误差。

2. 复杂系统：对于一些复杂的非线性系统，相平面法的分析可能会变得困难。

3. 定性分析：相平面法主要进行定性分析，难以进行定量计算。

非线性系统相平面法就像一把神奇的钥匙，能帮助我们打开非线性系统的神秘大门。通过相平面法，我们可以直观地了解系统的动态行为，为系统设计、信号处理、生物系统等领域提供有力支持。虽然相平面法存在一些局限性，但相信随着科学技术的不断发展，相平面法将会在更多领域发挥重要作用。让我们一起期待这个神奇的方法，为科学探索插上翅膀吧！