多自由度系统自由振动,多自由度系统自由振动原理与应用概述

你知道吗？在那些复杂的机械世界里，有一种系统特别引人注目，它就是多自由度系统。想象一个可以自由旋转、上下移动，甚至前后摆动的机械臂，这就是多自由度系统的典型代表。今天，我们就来聊聊这个神奇的系统，特别是它的自由振动特性。

什么是多自由度系统自由振动？

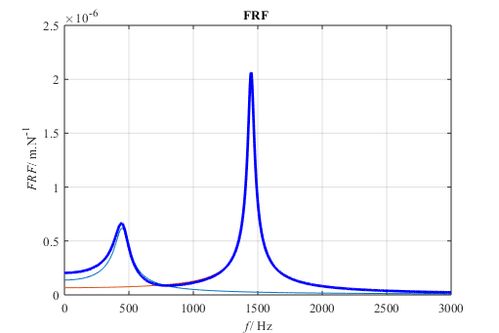
简单来说，多自由度系统自由振动就是指在没有外力作用下，系统依靠自身的弹性恢复力产生的振动。这种振动就像一个弹簧被压缩或拉伸后释放，它会自然地来回摆动。而在多自由度系统中，这种振动会同时在多个方向上发生。

多自由度系统自由振动的特点

1. 复杂性：由于多自由度系统涉及多个独立运动方向，因此其自由振动比单自由度系统要复杂得多。这就意味着，要准确描述和分析它的振动特性，我们需要用到更高级的数学工具。

2. 固有频率：每个自由度都有其固有的振动频率，就像弹簧的固有频率一样。这些固有频率决定了系统振动的快慢。

3. 振型：振型是指系统在振动过程中各部分相对位移的分布情况。在多自由度系统中，振型可能非常复杂，甚至会出现多个振型同时存在的现象。

多自由度系统自由振动的分析方法

1. 解析方法：这种方法主要适用于简单系统，通过建立系统的运动方程，然后求解方程得到振动特性。不过，对于复杂的多自由度系统，解析方法往往难以应用。

2. 数值方法：随着计算机技术的发展，数值方法成为研究多自由度系统自由振动的主要手段。常用的数值方法包括有限元法、模态分析等。

3. 实验方法：通过实验测量系统的振动特性，然后进行分析。这种方法可以直观地了解系统的振动行为，但实验成本较高。

多自由度系统自由振动的应用

1. 机械设计：在设计机械臂、机器人等设备时，需要考虑其自由振动特性，以确保设备在运行过程中的稳定性和可靠性。

2. 结构分析：在建筑、桥梁等结构设计中，需要分析结构的自由振动特性，以避免共振现象的发生。

3. 故障诊断：通过监测设备的振动信号，可以判断设备是否存在故障，从而提前进行维修。

多自由度系统自由振动的挑战

1. 复杂性：多自由度系统的自由振动特性非常复杂，难以用简单的数学模型描述。

2. 计算量：数值方法需要大量的计算资源，对于大型系统来说，计算量非常大。

3. 实验难度：实验方法需要专业的设备和技能，对于一些复杂系统来说，实验难度较高。

多自由度系统自由振动是一个充满挑战和机遇的领域。随着科技的不断发展，相信我们会有更多先进的工具和方法来研究这个领域，为我们的生活带来更多便利。让我们一起期待吧！