非线性系统相平面分析,非线性系统相平面分析方法解析与应用

你知道吗？在控制系统的世界里，有一种方法能让我们像侦探一样，揭开非线性系统的神秘面纱。它就是——相平面分析！今天，就让我带你一起走进这个奇妙的世界，看看相平面分析是如何让非线性系统变得透明起来的吧！

一、探秘非线性系统

非线性系统，听起来是不是有点高大上？其实，它就在我们身边。比如，你家里的洗衣机，就是一个典型的非线性系统。它的工作原理可不是简单的线性关系，而是充满了各种复杂的非线性特性。

那么，什么是非线性系统呢？简单来说，就是那些输出和输入不成正比的系统。在非线性系统中，一个微小的输入变化，可能会导致输出产生巨大的变化。这就让非线性系统变得难以捉摸，也让控制它们变得异常困难。

二、相平面分析：非线性系统的“X光片”

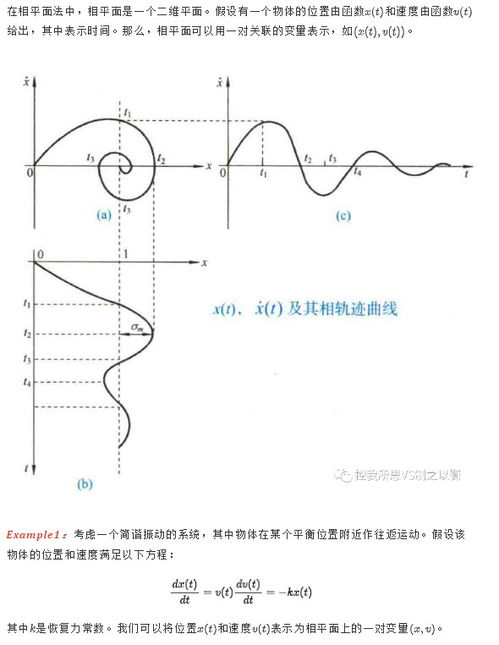
那么，如何才能看透非线性系统的本质呢？这时候，相平面分析就派上用场了。它就像一张“X光片”，能让我们清晰地看到非线性系统的内部结构。

相平面分析，顾名思义，就是在一个二维平面上，将系统的状态变量表示出来。在这个平面上，横坐标代表一个状态变量，纵坐标代表它的导数。这样一来，系统的动态行为就变成了一个轨迹，我们称之为相轨迹。

通过观察相轨迹，我们就能了解到系统的稳定性、平衡点、极限环等关键信息。是不是觉得神奇？其实，这就是相平面分析的魔力所在。

三、绘制相轨迹：非线性系统的“画像”

那么，如何绘制相轨迹呢？这里，我要介绍几种常用的方法：

1. 等倾线法：这种方法的核心思想是找到相平面上导数相同的点集，也就是等倾线。根据状态方程，我们可以得到等倾线的方程，进而绘制出相轨迹。

2. 直接积分法：这种方法直接对状态方程进行积分，得到相轨迹。

3. 数值方法：对于复杂的非线性系统，解析解往往难以获得。这时，我们可以采用数值方法，如Runge-Kutta法，来求解微分方程，得到相轨迹。

四、相平面分析的应用

相平面分析在工程实践中有着广泛的应用。以下是一些典型的应用场景：

1. 控制系统设计：通过相平面分析，我们可以设计出具有良好动态性能的控制系统。

2. 系统稳定性分析：相平面分析可以帮助我们判断系统的稳定性，避免系统出现不稳定现象。

3. 系统优化：通过调整系统参数，我们可以优化系统的性能，使其更加稳定、高效。

五、

相平面分析是一种强大的工具，能让我们深入理解非线性系统的动态行为。它不仅可以帮助我们设计出更好的控制系统，还能让我们在工程实践中避免许多潜在的风险。所以，让我们一起走进相平面分析的世界，探索非线性系统的奥秘吧！