二阶系统中,动态特性分析与优化设计

你知道吗？在那些复杂的控制系统里，有一个特别有趣的家伙，它就是二阶系统。听起来可能有点陌生，但别急，让我带你走进这个神秘的世界，一起探索二阶系统的奥秘吧！

二阶系统：一个充满活力的“小宇宙”

想象你手中拿着一个弹簧，轻轻一拉，然后松手。你会看到弹簧像个小精灵一样，先快速弹起，然后慢慢减速，最后平稳地回到原点。这个过程，其实就是二阶系统在自然界中的一个小小表演。

二阶系统，顾名思义，就是由二阶微分方程描述的系统。它不仅与当前的状态有关，还与过去的状态有关，就像一个有记忆的小精灵。这种特性使得二阶系统在自然界和工程技术领域里无处不在，比如机械振动、电路振荡、甚至人体内的生理过程。

数学建模：揭开二阶系统的神秘面纱

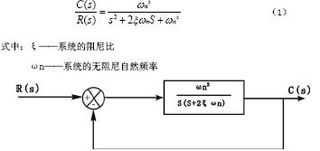
要深入了解二阶系统，我们得先学会用数学的语言来描述它。二阶系统的数学模型通常采用二阶线性微分方程，这个方程就像是一张地图，帮助我们找到系统响应的规律。

举个例子，一个简单的弹簧-质量-阻尼系统，可以用以下二阶微分方程来描述：

mx''(t) + cx'(t) + kx(t) = F(t)

在这个方程里，m代表质量，c代表阻尼系数，k代表弹簧常数，F(t)代表外部输入。通过这个方程，我们可以计算出弹簧在不同时间点的位置，就像预测未来一样神奇。

响应特性：二阶系统的“性格”

二阶系统的响应特性取决于它的参数，就像人的性格一样，千变万化。根据阻尼系数的不同，二阶系统可以分为三种状态：欠阻尼、临界阻尼和过阻尼。

欠阻尼：系统会像弹簧一样，先快速弹起，然后慢慢减速，最后平稳地回到原点。这种状态下的系统，就像一个活泼的孩子，充满活力。

临界阻尼：系统会迅速回到原点，没有振荡。这种状态下的系统，就像一个稳重的成年人，成熟稳重。

过阻尼：系统会缓慢地回到原点，没有振荡。这种状态下的系统，就像一个疲惫的老人，行动缓慢。

时域分析：二阶系统的“体检”

要了解二阶系统的性能，我们可以进行时域分析。时域分析就像给二阶系统做一次“体检”，通过观察系统的响应曲线，我们可以了解系统的稳定性、超调量、上升时间等性能指标。

举个例子，我们可以通过以下步骤进行时域分析：

1. 建立数学模型：根据实际情况，建立二阶系统的数学模型。

2. 求解微分方程：求解微分方程，得到系统的响应曲线。

3. 分析性能指标：根据响应曲线，分析系统的稳定性、超调量、上升时间等性能指标。

通过时域分析，我们可以对二阶系统有一个全面的认识，就像了解一个人的性格、健康状况一样。

：二阶系统，一个充满魅力的世界

二阶系统，就像一个充满魅力的世界，等待着我们去探索。通过数学建模、时域分析等方法，我们可以深入了解二阶系统的奥秘，为工程实践提供有力的理论支持。

在这个世界里，我们看到了欠阻尼系统的活力、临界阻尼系统的稳重、过阻尼系统的缓慢。这些特性使得二阶系统在自然界和工程技术领域里发挥着重要的作用。

所以，下次当你看到弹簧振动、电路振荡时，不妨想想二阶系统，也许你会对这个神秘的世界有更深的认识。