二阶系统稳定性,理论解析与工程应用综述

你知道吗？在控制系统的世界里，有一种系统特别受欢迎，它就像是个小明星，备受瞩目。它就是——二阶系统！今天，就让我带你走进这个神秘的世界，一起探索二阶系统的稳定性之谜吧！

二阶系统：控制界的明星

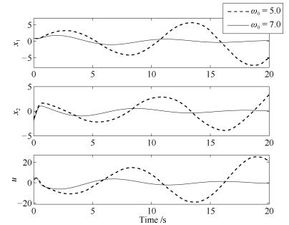
二阶系统，听起来是不是很高大上？其实，它就是由两个一阶系统组合而成的控制系统。别小看了它，在航空航天、工业自动化、机器人运动控制等领域，二阶系统可是大显身手呢！

稳定性：二阶系统的灵魂

稳定性，对于二阶系统来说，就像是它的灵魂。一个稳定的系统，就像是个安静的学霸，无论遇到什么困难，都能保持冷静，稳步前行。那么，如何判断一个二阶系统是否稳定呢？

特征根：稳定性的晴雨表

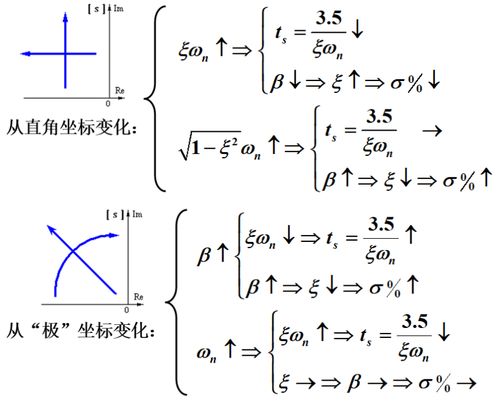
二阶系统的稳定性，可以通过它的特征根来判断。特征根，就像是二阶系统的指纹，每个系统都有自己独特的特征根。当特征根的实部全部为负时，系统就是稳定的；如果实部有正的，那可就麻烦了，系统可能会出现振荡、超调等问题。

阻尼比：稳定性的调节器

阻尼比，是衡量二阶系统稳定性的重要指标。它就像是个调节器，可以调整系统的稳定性。当阻尼比小于1时，系统处于欠阻尼状态，会出现振荡；当阻尼比等于1时，系统处于临界阻尼状态，没有振荡；当阻尼比大于1时，系统处于过阻尼状态，没有振荡，但响应速度较慢。

自然频率：稳定性的节奏

自然频率，是二阶系统的一个关键参数。它就像是个节奏，影响着系统的响应速度。自然频率越高，系统的响应速度越快；自然频率越低，系统的响应速度越慢。

MATLAB：稳定性分析的利器

MATLAB，这个强大的工具，可以帮助我们分析二阶系统的稳定性。通过MATLAB，我们可以绘制出系统的根轨迹、Bode图等，直观地了解系统的稳定性。

实例分析：稳定性在行动

让我们来看一个实例，看看稳定性是如何在行动中发挥作用的。

假设我们有一个二阶系统，其传递函数为：

\\[ G(s) = \\frac{K}{(s^2 + 2\\zeta\\omega_n s + \\omega_n^2)} \\]

其中，K是开环增益，\\(\\zeta\\)是阻尼比，\\(\\omega_n\\)是自然频率。

我们可以通过调整K、\\(\\zeta\\)和\\(\\omega_n\\)的值，来观察系统的稳定性变化。当K=1，\\(\\zeta=0.5\\)，\\(\\omega_n=1\\)时，系统处于欠阻尼状态，会出现振荡；当K=1，\\(\\zeta=1\\)，\\(\\omega_n=1\\)时，系统处于临界阻尼状态，没有振荡；当K=1，\\(\\zeta=1.5\\)，\\(\\omega_n=1\\)时，系统处于过阻尼状态，没有振荡，但响应速度较慢。

通过这个实例，我们可以看到，稳定性对于二阶系统来说是多么重要！

：稳定性，让二阶系统更精彩

稳定性，是二阶系统的灵魂。通过了解特征根、阻尼比、自然频率等参数，我们可以更好地掌握二阶系统的稳定性。MATLAB等工具，可以帮助我们分析二阶系统的稳定性。让我们一起努力，让二阶系统在控制界的舞台上更加精彩！