二阶惯性系统,控制理论在工程实践中的应用

你知道吗？在控制系统的世界里，有一个特别有趣的角色，它就是二阶惯性系统。听起来是不是有点高深？别急，让我带你一起探索这个神秘的世界，看看它到底有什么特别的地方。

什么是二阶惯性系统？

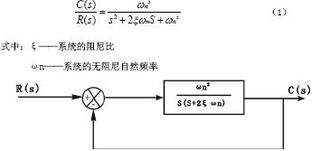
想象你手里拿着一个弹簧玩具，轻轻一推，它就会弹跳起来。这个玩具就是一个简单的二阶惯性系统。它由一个质量块、一个弹簧和一个阻尼器组成。当你推动玩具时，质量块会移动，弹簧会伸缩，阻尼器则会阻碍运动。这个过程，就是二阶惯性系统在发挥作用。

在数学上，二阶惯性系统可以用一个传递函数来描述。这个传递函数看起来可能有点复杂，但其实就是描述了系统输入和输出之间的关系。简单来说，它告诉我们，当系统受到一个输入信号时，它会怎么响应。

二阶惯性系统的特点

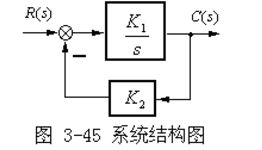
二阶惯性系统有几个特别的地方，让我们来一探究竟。

1. 时间常数

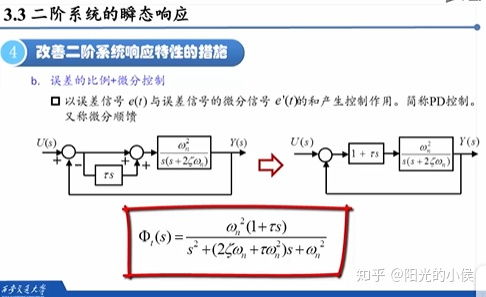
时间常数是描述系统响应速度的一个重要参数。它告诉我们，系统需要多长时间才能达到稳定状态。时间常数越小，系统响应越快。

2. 阻尼比

阻尼比是描述系统阻尼程度的一个参数。它告诉我们，系统在运动过程中，会有多快的衰减。阻尼比越大，系统衰减越快。

3. 自然频率

自然频率是描述系统固有振动频率的一个参数。它告诉我们，系统在没有外力作用时，会以多快的速度振动。自然频率越高，系统振动越快。

二阶惯性系统的应用

二阶惯性系统在现实生活中有着广泛的应用。比如，汽车悬挂系统、机器人关节、空调系统等等，都离不开二阶惯性系统的身影。

1. 汽车悬挂系统

汽车悬挂系统是一个典型的二阶惯性系统。它通过弹簧和阻尼器来吸收路面颠簸，保证车辆的平稳行驶。

2. 机器人关节

机器人关节也是一个二阶惯性系统。它通过精确控制关节的运动，使机器人能够完成各种复杂的动作。

3. 空调系统

空调系统也是一个二阶惯性系统。它通过控制压缩机的工作，调节室内温度，保证人们的生活舒适。

二阶惯性系统的仿真

为了更好地理解二阶惯性系统，我们可以通过仿真来观察它的动态特性。

1. MATLAB仿真

MATLAB是一款强大的仿真软件，可以用来模拟二阶惯性系统的动态特性。通过MATLAB，我们可以观察系统在不同参数下的响应曲线，分析系统的稳定性、超调量等性能指标。

2. PID控制器

PID控制器是一种常用的控制算法，可以用来调整二阶惯性系统的参数，使其达到最佳性能。通过MATLAB仿真，我们可以观察PID控制器对系统性能的影响，找到最佳的控制器参数。

二阶惯性系统是一个充满魅力的控制系统，它广泛应用于我们的生活中。通过了解二阶惯性系统的特点和应用，我们可以更好地理解控制系统的原理，为未来的创新和发展打下坚实的基础。所以，下次当你看到一辆汽车行驶在道路上，或者一台机器人完成一个复杂的动作时，不妨想想，这背后离不开二阶惯性系统的默默付出。