给定系统微分方程,解析与数值解法在科学计算中的应用

亲爱的读者们，你是否曾在某个深夜，对着复杂的微分方程挠头抓耳？别担心，今天我要带你一起探索这个神秘的世界，揭开给定系统微分方程的神秘面纱。让我们一起踏上这场数学之旅，感受微分方程的魅力吧！

一、微分方程：揭秘动态世界的密码

微分方程，这个看似高深莫测的数学工具，其实在我们的生活中无处不在。它就像一把钥匙，能解锁动态世界的密码。从简单的弹簧振子到复杂的生态系统，微分方程都能帮助我们理解这些系统的运行规律。

想象一个弹簧振子，它的运动可以用一个二阶微分方程来描述。这个方程告诉我们，振子的运动速度和加速度是如何随着时间变化的。通过解这个方程，我们就能预测振子的未来运动轨迹。

二、给定系统微分方程：探索未知世界的窗口

给定系统微分方程，就像一扇窗户，让我们窥视未知世界的奥秘。它不仅揭示了系统的内在规律，还能帮助我们预测系统的未来行为。

以一个简单的电路为例，我们可以用微分方程来描述电路中电流和电压的变化。通过解这个方程，我们就能了解电路的稳定性，预测电路在受到干扰时的响应。

三、求解给定系统微分方程：一场数学的冒险

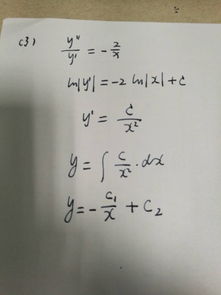
求解给定系统微分方程，就像一场数学的冒险。在这个过程中，我们需要运用各种数学技巧，如分离变量法、常数变易法等。

以一个常见的微分方程为例：y'' + py' + qy = f(t)。这个方程描述了一个二阶线性常系数微分方程。为了解这个方程，我们首先需要找到它的齐次解，即满足微分方程的解。我们需要根据输入信号f(t)来确定特解，即满足微分方程和初始条件的解。

这个过程就像解一个谜题，需要我们仔细分析问题，运用各种数学工具，最终找到答案。

四、微分方程的应用：无处不在的数学魔法

微分方程的应用范围非常广泛，几乎涵盖了所有科学和工程领域。以下是一些常见的应用场景：

1. 物理学：描述物体的运动、振动、波动等现象。

2. 生物学：研究种群动态、生态系统平衡等问题。

3. 工程学：分析电路、控制系统、机械系统等。

4. 经济学：研究市场动态、经济增长等问题。

微分方程就像一把神奇的魔法棒，能帮助我们解决各种实际问题。

五、：微分方程，开启未知世界的钥匙

通过本文的介绍，相信你已经对给定系统微分方程有了更深入的了解。微分方程，这个看似高深莫测的数学工具，其实就在我们的身边。它就像一把钥匙，能解锁未知世界的密码，帮助我们探索这个世界的奥秘。

让我们一起继续探索这个充满魅力的数学世界，感受微分方程带来的无限可能吧！