非线性系统的数学模型,非线性系统数学模型构建方法探讨

你知道吗？在控制理论的世界里，有一个特别神奇的东西，它就像一个谜一样，让人既着迷又困惑。这就是非线性系统的数学模型。想象你手中拿着一个复杂的机械玩具，它有各种各样的运动方式，而这些运动方式又似乎没有固定的规律。这就是非线性系统，而数学模型就是那个能帮你解开谜团的神奇工具。

非线性系统的魅力

非线性系统，听起来是不是有点高大上？其实，它就在我们身边。比如，你家里的空调，当你调整温度时，它的制冷效果并不是线性变化的；再比如，你骑自行车，当你加速时，速度的增加也不是线性的。这些现象，都是非线性系统的典型表现。

非线性系统的魅力在于它的复杂性和多样性。它不像线性系统那样简单，线性系统就像一条直线，简单明了。而非线性系统，就像一幅复杂的画卷，充满了变化和可能性。

数学模型：非线性系统的解码器

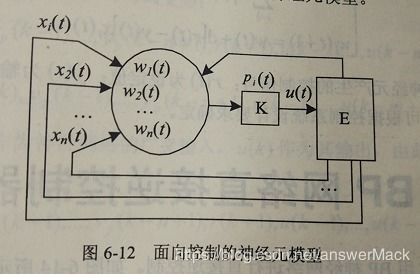
那么，如何才能理解非线性系统呢？这就需要用到数学模型。数学模型，就像是给非线性系统穿上了一件“外衣”，让我们可以从数学的角度去观察和理解它。

数学模型有很多种，比如微分方程、传递函数、状态空间模型等等。这些模型，都是通过数学公式来描述系统的输入输出关系，从而帮助我们理解系统的行为。

微分方程：非线性系统的语言

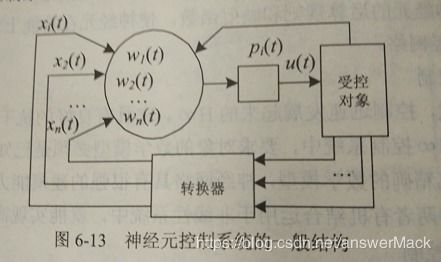
微分方程，是描述非线性系统最常用的数学工具之一。它就像是一把钥匙，能打开非线性系统的神秘之门。

比如，一个简单的非线性系统，可以用以下微分方程来描述：

\\[ \\frac{dx}{dt} = -x^2 + u \\]

这个方程中，\\( x \\) 表示系统的状态，\\( u \\) 表示系统的输入。通过这个方程，我们可以计算出系统在不同时间点的状态。

当然，现实中的非线性系统要复杂得多，可能需要用到多个微分方程来描述。但不管怎样，微分方程都是理解非线性系统的重要工具。

传递函数：非线性系统的抽象

传递函数，是另一种描述非线性系统的数学工具。它通过将系统的输入输出关系转化为一个数学函数，从而简化了系统的分析。

比如，一个简单的非线性系统，可以用以下传递函数来描述：

\\[ H(s) = \\frac{1}{s^2 + 1} \\]

这个函数中，\\( s \\) 是复数频率，\\( H(s) \\) 表示系统的传递函数。通过这个函数，我们可以计算出系统在不同频率下的响应。

传递函数的优点是，它可以将非线性系统转化为线性系统进行分析，从而简化了计算。

状态空间模型：非线性系统的全面描述

状态空间模型，是描述非线性系统最全面的方法之一。它通过建立系统的状态方程和输出方程，将系统的输入输出关系完整地描述出来。

比如，一个简单的非线性系统，可以用以下状态空间模型来描述：

\\[ \\begin{cases}

\\dot{x}_1 = -x_1^2 + u \\\\

\\dot{x}_2 = x_1

\\end{cases} \\]

\\[ y = x_1

这个模型中，\\( x_1 \\) 和 \\( x_2 \\) 是系统的状态，\\( u \\) 是系统的输入，\\( y \\) 是系统的输出。通过这个模型，我们可以计算出系统在不同时间点的状态和输出。

状态空间模型的优势在于，它能够全面地描述非线性系统的行为，从而为系统的分析和设计提供了有力的工具。

非线性系统的挑战与机遇

非线性系统的数学模型，虽然能够帮助我们理解系统的行为，但同时也带来了挑战。因为非线性系统的复杂性，使得数学模型的建立和分析变得困难。

正是这种挑战，也带来了机遇。随着计算机技术的发展，我们可以利用计算机来辅助我们进行非线性系统的建模和分析。同时，随着人工智能技术的进步，我们可以利用机器学习等方法来预测非线性系统的行为，从而为系统的优化和控制提供了新的思路。

非线性系统的数学模型，就像是一把钥匙，能帮助我们打开非线性世界的神秘之门。在这个充满挑战和机遇的世界里，让我们一起探索，一起成长吧！