负反馈系统的开环传递函数,负反馈系统开环传递函数解析与应用

你知道吗？在自动控制的世界里，有一个神奇的小玩意儿，它叫做“负反馈系统的开环传递函数”。听起来是不是有点儿高深莫测？别急，让我带你一探究竟，揭开它的神秘面纱。

负反馈，你了解多少？

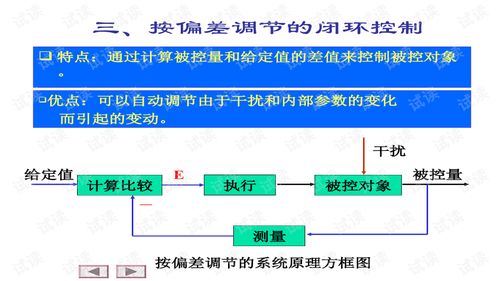
想象你正在玩一个游戏，目标是让屏幕上的小球保持在中心位置。每当小球偏离中心，你就要调整方向，让小球回到中心。这个过程，就像是负反馈在自动控制系统中的作用。它不断地监测系统的输出，然后调整输入，以确保输出尽可能接近期望值。

在负反馈系统中，有一个非常重要的概念，那就是“开环传递函数”。它描述了系统在没有反馈的情况下，输入信号到输出信号之间的传递关系。简单来说，就是输入信号如何影响输出信号。

开环传递函数，揭秘！

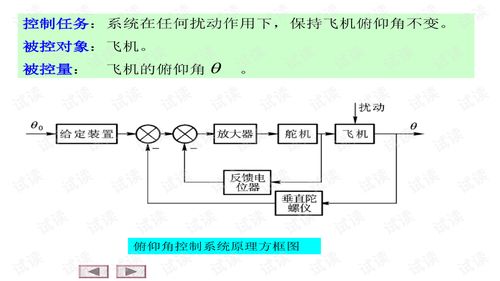
好啦，现在让我们来具体看看这个开环传递函数。假设你有一个系统，它的输入是R(s)，输出是C(s)，前向通道传递函数是G1(s)和G2(s)，反馈通道传递函数是H(s)。那么，这个系统的开环传递函数G(s)就可以表示为：

G(s) = G1(s) G2(s) H(s)

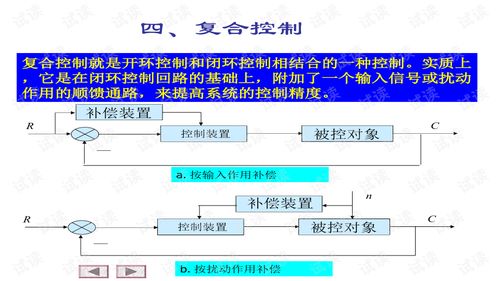
这里的H(s)等于1，因为我们是讨论单位负反馈系统。所以，G(s)实际上就是前向通道传递函数的乘积。

稳定性，关键所在

你知道吗？一个系统的稳定性，很大程度上取决于它的开环传递函数。怎么判断呢？这就需要用到劳斯判据了。劳斯判据是一种判断系统稳定性的方法，它通过分析开环传递函数的极点来判断系统是否稳定。

简单来说，如果一个系统的开环传递函数的极点全部位于复平面的左半部分，那么这个系统就是稳定的。反之，如果极点有位于右半部分的，那么系统就是不稳定的。

实例分析，让你一目了然

来，让我们通过一个具体的例子来加深理解。假设有一个单位负反馈系统的开环传递函数为：

G(s) = K(s + 2) / [s(s + 4)(s + 10)]

我们要确定系统稳定时K的值范围。首先，我们需要找到这个系统的闭环传递函数。闭环传递函数可以通过以下公式计算：

Gc(s) = G(s) / [1 + G(s)]

将G(s)代入上式，我们得到：

Gc(s) = K(s + 2) / [s(s + 4)(s + 10) + K(s + 2)]

接下来，我们需要使用劳斯判据来判断系统稳定性。通过分析闭环传递函数的分母，我们可以得到以下劳斯表：

| s^3 | s^2 | s^1 | s^0 |

| --- | --- | --- | --- |

| 1 | K | 2K | 0 |

| 1 | 1 | 4 | 10 |

| 1 | 1 | 1 | 0 |

根据劳斯判据，如果劳斯表中所有主对角线上的元素都大于0，那么系统就是稳定的。在这个例子中，我们可以看到，当K大于0时，劳斯表中所有主对角线上的元素都大于0，因此系统是稳定的。

负反馈系统的开环传递函数

通过这篇文章，我们了解了负反馈系统的开环传递函数，以及它如何影响系统的稳定性。希望这篇文章能帮助你更好地理解自动控制的世界。记住，负反馈系统的开环传递函数，就像是自动控制系统的“灵魂”，它决定了系统的性能和稳定性。所以，让我们一起探索这个神秘的世界吧！