二阶线性系统,特性、分析与仿真应用

你知道吗？在控制工程的世界里，有一种系统特别引人注目，它就像一个优雅的舞者，时而轻盈跳跃，时而稳重前行。它就是——二阶线性系统！今天，就让我带你走进这个神秘的世界，一起揭开它的面纱。

二阶线性系统的“前世今生”

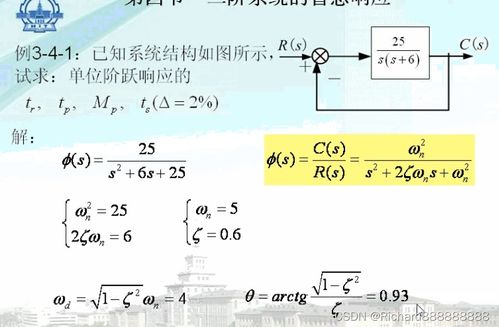
二阶线性系统，听起来是不是有点高大上？其实，它就是由二阶微分方程描述的系统。简单来说，就是那种涉及到变量二次导数的动态系统。别看它名字里有个“二阶”，但它在实际应用中可是无处不在，比如汽车悬挂系统、电子电路、机械臂控制等等。

你知道吗？二阶线性系统还有一个特点，那就是它包含两个独立的状态变量。这就意味着，它能够描述系统在任意时刻的状态，就像一个侦探，能够追踪到系统的每一个细节。

二阶线性系统的“性格特点”

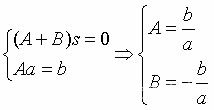
二阶线性系统就像一个多面手，有着不同的性格特点。它可以是稳重的，也可以是活泼的，甚至有时候还会有些“小情绪”。

1. 欠阻尼系统：这种系统就像一个充满活力的小姑娘，总是跳来跳去，无法安静下来。当它受到外界干扰时，会先超过目标值，然后又从峰值开始下降，呈现减幅振荡，最终趋于目标值。

2. 过阻尼系统：这种系统就像一个稳重的老者，总是脚踏实地，稳步前行。当它受到外界干扰时，会单调地趋于目标值，不会出现振荡。

3. 临界阻尼系统：这种系统就像一个恰到好处的舞者，既不会过于活泼，也不会过于沉稳。当它受到外界干扰时，会以最短的时间趋于目标值，不会出现振荡。

二阶线性系统的“数学模型”

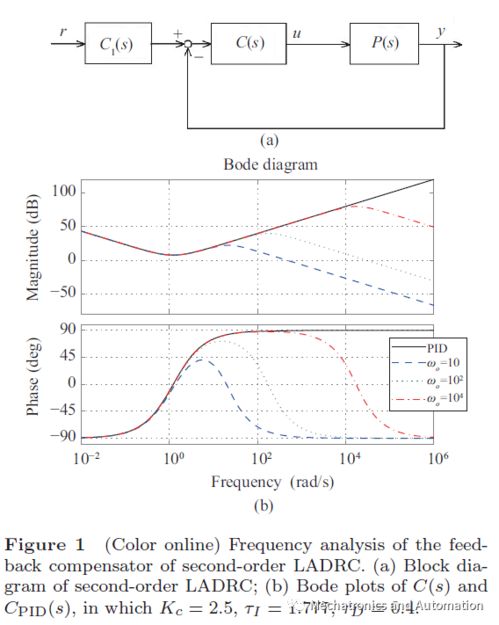
二阶线性系统的数学模型通常采用二阶线性微分方程。这种方程描述了系统的输出与输入之间的关系，以及系统的动态行为。方程中的参数，比如质量、阻尼、弹簧常数等，就像系统的DNA，决定了系统的响应特性。

二阶线性微分方程的一般形式为：\\[ a_2 \\frac{d^2y}{dt^2} + a_1 \\frac{dy}{dt} + a_0 y = b_1 x(t) + b_0 u(t) \\]

其中，\\( y \\) 是系统的输出，\\( x(t) \\) 是系统的输入，\\( u(t) \\) 是系统的控制信号，\\( a_2, a_1, a_0, b_1, b_0 \\) 是系统的参数。

二阶线性系统的“MATLAB之旅”

MATLAB，这个强大的工具箱，可以帮助我们更好地分析和仿真二阶线性系统。通过MATLAB，我们可以绘制系统的阶跃响应曲线、频率响应曲线，甚至可以设计控制器来优化系统的性能。

比如，我们可以使用MATLAB中的`step`函数来绘制系统的阶跃响应曲线，通过观察曲线的形状，我们可以判断系统的稳定性、超调量、上升时间等性能指标。

二阶线性系统的“未来展望”

随着科技的不断发展，二阶线性系统在各个领域的应用越来越广泛。未来，它将在自动驾驶、智能机器人、航空航天等领域发挥越来越重要的作用。

二阶线性系统就像一个充满魅力的舞者，它优雅、稳重、充满活力。让我们一起期待，这个舞者在未来的舞台上，将带来更多精彩的表演！