二阶系统的阶跃响应,特性、影响因素与动态行为

你知道吗？在控制工程的世界里，有一种系统特别有趣，它就像一个跳动的音符，时而欢快，时而沉稳，这就是——二阶系统的阶跃响应。想象你按下了一个按钮，系统就像一个舞者，开始了一段精彩的舞蹈。接下来，就让我们一起揭开这个神秘舞者的面纱，看看它的阶跃响应到底有多精彩吧！

一、二阶系统的“舞步”解析

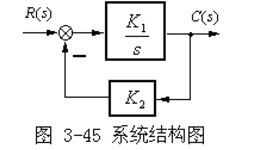
二阶系统，听起来是不是很高大上？其实，它就是由二阶微分方程描述的系统。别被这些复杂的术语吓到，简单来说，它就是一个在受到激励信号后，响应随时间变化呈现出特定规律的“舞者”。

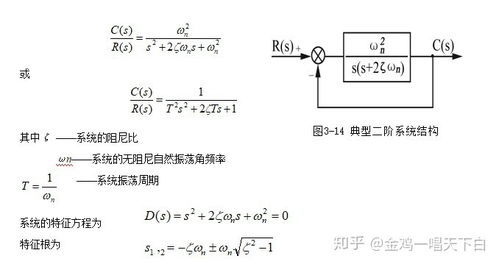
要了解二阶系统的阶跃响应，首先得知道它的“舞步”是如何形成的。这就要提到一个重要的参数——传递函数。传递函数就像一个指挥棒，指挥着系统如何“跳舞”。对于二阶系统，它的传递函数通常长这样：

\\[ G(s) = \\frac{K}{(s^2 + 2\\zeta\\omega_n s + \\omega_n^2)} \\]

其中，\\( K \\) 是系统的增益，\\( \\zeta \\) 是阻尼比，\\( \\omega_n \\) 是无阻尼自然频率。这三个参数就像二阶系统的“三件宝”，决定了它的“舞步”风格。

二、阶跃响应的“舞姿”展现

当二阶系统受到阶跃输入信号时，它的输出会随时间变化，这个过程就是阶跃响应。根据阻尼比的不同，阶跃响应可以分为四种情况：

1. 欠阻尼系统：当 \\( 0 < \\zeta < 1 \\) 时，系统会出现振荡衰减的响应，就像一个翩翩起舞的少女，时而轻盈，时而沉稳。

2. 临界阻尼系统：当 \\( \\zeta = 1 \\) 时，系统会出现无超调、无振荡的单调上升响应，就像一个稳健的舞者，步伐坚定，节奏稳健。

3. 过阻尼系统：当 \\( \\zeta > 1 \\) 时，系统会出现无超调、无振荡的单调上升响应，但上升速度较慢，就像一个沉稳的舞者，步伐缓慢，但始终向前。

4. 无阻尼系统：当 \\( \\zeta = 0 \\) 时，系统会出现持续的等幅振荡响应，就像一个永不停歇的舞者，永远在跳动。

三、阶跃响应的“舞者”魅力

二阶系统的阶跃响应不仅具有丰富的“舞姿”，还具有许多独特的魅力：

1. 稳定性：阶跃响应的稳定性取决于阻尼比的大小。当 \\( \\zeta < 1 \\) 时，系统是稳定的；当 \\( \\zeta = 1 \\) 时，系统是临界稳定的；当 \\( \\zeta > 1 \\) 时，系统是不稳定的。

2. 快速性：阶跃响应的快速性取决于无阻尼自然频率的大小。当 \\( \\omega_n \\) 越大时，系统响应越快。

3. 平稳性：阶跃响应的平稳性取决于阻尼比的大小。当 \\( \\zeta \\) 接近 1 时，系统响应越平稳。

4. 超调量：阶跃响应的超调量是指系统响应的最大峰值与稳态值之比。当 \\( \\zeta < 1 \\) 时，系统会出现超调现象。

四、阶跃响应的“舞者”应用

二阶系统的阶跃响应在控制工程领域有着广泛的应用，比如：

1. 伺服系统：在伺服系统中，二阶系统的阶跃响应可以用来控制执行机构的运动速度和位置。

2. 滤波器：在滤波器中，二阶系统的阶跃响应可以用来滤除信号中的噪声。

3. 振动控制：在振动控制中，二阶系统的阶跃响应可以用来抑制系统的振动。

4. 机器人控制：在机器人控制中，二阶系统的阶跃响应可以用来控制机器人的运动轨迹。

二阶系统的阶跃响应就像一个充满魅力的舞者，它的舞姿优美，舞步稳健，为控制工程领域带来了无尽的惊喜。让我们一起欣赏这个舞者的精彩表演吧！