复动力系统,复动力系统理论与实践解析

探索复动力系统的奇妙世界：一场数学与美学的邂逅

想象你手中握着一枚神奇的魔方，每一个转动都带来全新的图案。这就是复动力系统，一个充满魔力的数学世界，它将带你领略数学与美学的完美邂逅。

一、复动力系统的起源与魅力

复动力系统，顾名思义，是研究复数域上的动力系统。它起源于17世纪，当时牛顿用迭代法求多项式的近似零点。20世纪初，法国数学家Fatou和Julia开始研究黎曼球面上的有理函数的迭代，从而开启了复动力系统的研究之旅。

复动力系统的魅力在于，它将数学的严谨与美学的韵味完美结合。在这个世界里，你可以看到美丽的分形图案，感受到数学的无限魅力。

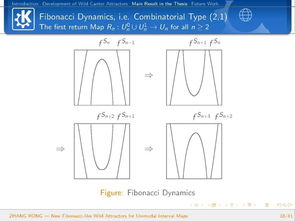
二、Fatou集与Julia集：复动力系统的灵魂

Fatou集和Julia集是复动力系统中的两个重要概念。Fatou集是指对于任意一个点，其迭代序列要么收敛于一个不动点，要么趋于一个极限环。而Julia集则是指Fatou集的补集。

Fatou集和Julia集的形状各异，有的像花朵，有的像火焰，有的像山脉。这些美丽的图案让人不禁感叹数学的神奇。

三、复动力系统的应用：从理论到实践

复动力系统不仅在数学领域有着广泛的应用，还渗透到了其他学科。例如，在通信领域，复混沌系统可以提高信息传输的安全性；在生物学领域，复动力系统可以用来研究生物种群的数量变化。

此外，复动力系统在金融、物理、化学等领域也有着广泛的应用。可以说，复动力系统已经成为现代科学研究中不可或缺的一部分。

四、复动力系统的挑战与未来

尽管复动力系统在各个领域都有着广泛的应用，但仍然面临着许多挑战。例如，如何更好地理解复动力系统的复杂行为，如何将其应用于实际问题中。

未来，随着数学、计算机科学等领域的不断发展，复动力系统的研究将会更加深入。我们有理由相信，复动力系统将会在更多领域发挥重要作用。

五、：走进复动力系统的奇妙世界

复动力系统是一个充满魔力的数学世界，它将带你领略数学与美学的完美邂逅。在这个世界里，你可以看到美丽的分形图案，感受到数学的无限魅力。让我们一起走进复动力系统的奇妙世界，探索数学的奥秘吧！