非自治系统的稳定性,非自治系统稳定性研究进展与挑战

亲爱的读者们，你是否曾在某个午后，坐在窗边，看着窗外的树叶随风摇曳，心中不禁涌起对自然规律的无限遐想？今天，我们就来聊聊这样一个话题——非自治系统的稳定性。想象那些看似杂乱无章的自然现象，其实都遵循着一定的规律，而我们要做的，就是揭开这神秘的面纱。

什么是非自治系统？

非自治系统，顾名思义，就是那些与时间有关的系统。它们的特点是，系统的状态不仅取决于当前的状态，还与时间有关。换句话说，非自治系统的行为会随着时间的变化而变化。举个例子，地球绕太阳公转，就是一个典型的非自治系统。地球的位置不仅取决于它当前的位置，还取决于它已经绕太阳转了多少圈。

非自治系统的稳定性

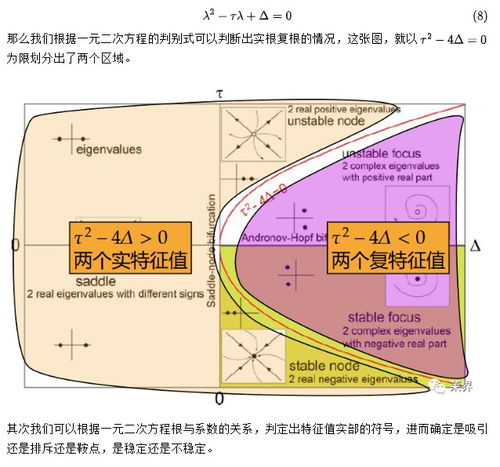
稳定性，是描述系统在受到扰动后能否恢复到原来状态的一个概念。对于非自治系统来说，稳定性尤为重要。因为一旦系统失去稳定性，后果可能不堪设想。那么，如何判断一个非自治系统是否稳定呢？

首先，我们要了解什么是平衡点。平衡点，就是系统在不受任何扰动时，能够保持静止或匀速直线运动的状态。对于非自治系统来说，平衡点可能随着时间的变化而变化。因此，我们需要考虑平衡点的稳定性。

稳定平衡点，是指系统在受到扰动后，能够逐渐恢复到原来的平衡状态。而不稳定平衡点，则是指系统在受到扰动后，会逐渐偏离原来的平衡状态。那么，如何判断一个平衡点是稳定还是不稳定的呢？

我们可以通过观察系统的状态方程来判断。如果状态方程在平衡点附近的变化是单调的，那么这个平衡点就是稳定的。反之，如果状态方程在平衡点附近的变化是非单调的，那么这个平衡点就是不稳定的。

非自治系统的稳定性分析

非自治系统的稳定性分析，是一个复杂而有趣的过程。在这个过程中，我们需要运用各种数学工具，如Lyapunov稳定性理论、指数稳定性理论等。

Lyapunov稳定性理论，是一种常用的稳定性分析方法。它通过构造一个Lyapunov函数，来判断系统的稳定性。如果Lyapunov函数在平衡点附近是负定的，那么系统就是稳定的。

指数稳定性理论，则是一种更严格的分析方法。它要求系统在受到扰动后，能够以指数速度收敛到平衡点。这种稳定性被称为指数稳定性。

在实际应用中，非自治系统的稳定性分析具有重要意义。例如，在控制理论中，我们需要确保控制系统在受到扰动后，能够稳定地运行；在生物系统中，我们需要了解生物种群在受到外界干扰后的动态变化。

非自治系统的稳定性研究现状

近年来，随着科学技术的不断发展，非自治系统的稳定性研究取得了许多重要成果。以下是一些值得关注的进展：

1. 非自治系统的指数稳定性分析：研究者们提出了许多关于非自治系统指数稳定性的充分条件，为实际应用提供了理论指导。

2. 非自治系统的鲁棒稳定性分析：在考虑系统参数不确定性和外部干扰的情况下，研究者们研究了非自治系统的鲁棒稳定性问题。

3. 非自治系统的全局稳定性分析：研究者们提出了许多关于非自治系统全局稳定性的充分条件，为实际应用提供了理论指导。

4. 非自治系统的数值模拟：随着计算机技术的不断发展，研究者们可以利用数值模拟方法，对非自治系统的稳定性进行更深入的研究。

非自治系统的稳定性研究是一个充满挑战和机遇的领域。相信在不久的将来，随着科学技术的不断发展，我们能够揭开更多关于非自治系统稳定性的奥秘。