工程信号与系统,现代通信与电子技术基石

揭秘工程信号与系统的奇妙世界

想象你手中拿着一部手机，轻轻一点，就能与远在千里之外的朋友畅谈。这背后，隐藏着一个神奇的领域——工程信号与系统。它就像一位默默无闻的魔术师，将我们的声音、图像等信息，通过一系列复杂的变换，传递到世界的每一个角落。今天，就让我们一起走进这个奇妙的世界，揭开它的神秘面纱。

信号：信息的载体

信号，是信息的载体，它可以是声音、图像、温度、压力等各种物理量的变化。在工程领域，信号分为两大类：模拟信号和数字信号。

模拟信号，就像一条平滑的曲线，它在时间和幅度上都是连续的。比如，我们日常生活中的电话通话、广播信号等，都属于模拟信号。

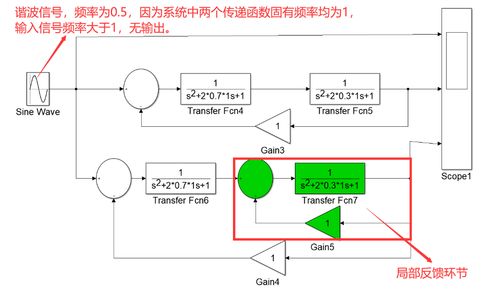
数字信号，则像一串串跳动的数字，它在时间和幅度上都是离散的。比如，我们手机中的短信、网络数据等，都属于数字信号。

系统：信号的处理器

系统，是处理信号的设备或算法。它可以将输入的信号进行放大、滤波、调制、解调等操作，最终输出我们需要的信号。

在工程信号与系统中，线性时不变（LTI）系统占据着重要的地位。LTI系统具有以下特点：

1. 线性：系统对信号的叠加和尺度变换具有线性关系。

2. 时不变：系统的特性不随时间变化。

LTI系统在通信、图像处理、音频处理等领域有着广泛的应用。

傅里叶变换：信号的频域分析

傅里叶变换，是分析信号频域特性的重要工具。它可以将信号从时域转换到频域，帮助我们更好地理解信号的组成。

傅里叶变换的基本原理是将信号分解为一系列正弦波和余弦波的叠加。通过分析这些正弦波和余弦波的频率、幅度和相位，我们可以了解信号的频谱特性。

例如，在音频处理中，傅里叶变换可以帮助我们分析声音的频率成分，从而实现降噪、回声消除等功能。

拉普拉斯变换：控制系统的灵魂

拉普拉斯变换，是控制系统设计中的关键工具。它可以将线性微分方程转换为代数方程，从而简化控制系统的分析。

在控制系统设计中，拉普拉斯变换可以帮助我们分析系统的稳定性、动态性能等特性。通过调整系统参数，我们可以使系统达到预期的性能。

采样定理：数字信号处理的基石

采样定理，是数字信号处理中的基本原理。它指出，只要采样频率足够高，就可以从采样信号中恢复出原始的连续信号。

采样定理的数学表达式为：采样频率必须大于信号最高频率的两倍。

采样定理的发现，为数字信号处理技术的发展奠定了基础。

工程信号与系统的应用

工程信号与系统在各个领域都有着广泛的应用，以下列举几个例子：

1. 通信：在通信领域，信号与系统用于信号的调制、解调、传输和接收。

2. 图像处理：在图像处理领域，信号与系统用于图像的压缩、增强、分割等。

3. 音频处理：在音频处理领域，信号与系统用于音频的降噪、回声消除、音质提升等。

4. 控制系统：在控制系统领域，信号与系统用于系统的设计、分析和优化。

工程信号与系统，是一个充满神奇和挑战的领域。它不仅为我们的生活带来了便利，还为科技的发展提供了强大的动力。让我们一起走进这个奇妙的世界，探索它的无限可能吧！